蜘蛛网:正确的轮比和笔画长度?
轮毂大小和笔画长度的比率是多少,才能在螺旋线上完成一圈。也就是说,具有以下特征的螺旋仪:
3侧= 1.5 : 4pi (轮对比:笔长)
4面= 1.333 :6
5面= 2.5 :5
(A)为什么1.2/10和6/2都要做6面螺旋图?
(A)比率是多少?
(C)我如何做一个八角形螺旋图?
function spiro ( N:float,k:int ): Vector3//spirograph loop, N=total points in loop, k=current loop
{ //wr,pr=wheel/pen ratio: 5, 3, 4, 6, 6,
var wr:float[]=new float[10];wr[0]=2.5;wr[1]=1.5;wr[2]=1.33333;wr[3]=1.2;wr[4]=6;
var pr:float[]=new float[10];pr[0]=5.0;pr[1]=4.0;pr[2]=6.00000;pr[3]=10; pr[4]=2;
var vr = 4;
var wheel=wr[vr];
var theta =(1/N)*Mathf.PI *pr[vr]*k;
var rtheta =theta*wheel;
var small = (1-1/wheel);//
var cx=Mathf.Cos(theta)*small;
var cz=Mathf.Sin(theta)*small;
var ex=Mathf.Cos(theta-rtheta)/wheel;
var ez=Mathf.Sin(theta-rtheta)/wheel;
return Vector3(cx+ex,0,cz+ez);
}回答 2
Stack Overflow用户
发布于 2014-03-14 13:25:51
在MathWorld关于螺旋图和下胚轴的文章中,有一些非常好的图片,可以更容易地描述正在发生的事情。
特设解释
对于特定数目的“边”,外半径(R)与内半径(r)之间的比值很容易计算出来。从小圆的中心到“笔”的距离决定了形状的边是“块状”的。
sides = R / r看一看方程的形式是有指导意义的,而不需要为所要求的八边样本编写c代码“妨碍”。在Mathematica中,这可以写成:
hypotrochoid[R_, r_, h_] := Function[t, {
(R - r) Cos[t] + h Cos[(R - r) t/r],
(R - r) Sin[t] - h Sin[(R - r) t/r]
}]
ParametricPlot[hypotrochoid[1, 1/8, 1/40][t], {t, 0, 2 \[Pi]}]

笔画长度
要计算笔画长度,您需要两条信息。1)函数的周期;2)曲线在单个周期内的弧长。
有一个很好的解释,在math.stackexchange上的一个周期,但在这种情况下,你所描述的周期将是2π。在更一般的情况下,如果R和r都是理性,则周期是有限的,并且是2pi的倍数。
您可以根据参数曲线弧长的表达式找到笔画长度。
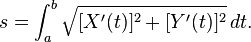
在下弦方程中替换(简化一些,假设周期为2pi),最后得到弧长的表达式:
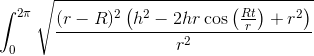
通过检验,我相信在R,r和h上有适当的约束条件,你应该能够得到一个解析解(可能是一个完全椭圆积分族)。如果你得到了R,r和h的值,那么一个好的计算机代数系统(CAS)就会找到一个解。
不管您是否有CAS,对于近乎多边形的螺旋图,弧长方程非常简单,可以使用朴素方法(Euler Integration)来求解。
Stack Overflow用户
发布于 2014-03-28 08:38:35
8面螺旋仪笔的线长,如果笔位于小轮的边缘,则为小轮半径的8倍。6、5、4等
多边形也可以以这种方式以三角方式绘制:http://1ucasvb.tumblr.com/post/42906053623/in-a-previous-post-i-showed-how-to-geometrically。
下面是Plotter函数中的一个演示。https://functionplotter.com/#W3sidHlwZSI6MCwiZXEiOiIoc2VjKCgyLzYpKmFzaW4oc2luKCg2LzIpKngpKSkpKnNpbih4KSIsImNvbG9yIjoiIzAwMDAwMCJ9LHsidHlwZSI6MTAwMH1d
https://stackoverflow.com/questions/22383692
复制相似问题

