沙-1碰撞概率
我很难在纸上和脑子里解决这个问题。我知道这是围绕生日悖论,然而,我似乎无法理解我的问题和BP的解决方案之间的价值互换性。
好的,我知道SHA-1会产生160位的散列。
在两条消息和0.5的概率之间,所述“攻击者”必须搜索多少次才能找到相同的哈希值?
我从搜索中找到了一系列的解决方案,但没有一种方法能让我彻底理解这个过程,并以一种对我来说有意义的方式来解释它。下面是我在搜索过程中能找到的最接近的。
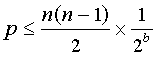
我希望这能解释我的问题。
Stack Overflow用户
发布于 2015-10-14 15:56:19
是的,你是对的;这是绕着生日问题转的。在散列过程中,您实际上是试图通过一个数学过程将理论上无限长的东西放置到一个固定长度的字符串中;因此,碰撞是不可避免的。
生日问题基本上意味着假设你有一个满是人的大厅,你会问每个人他们的出生日期。当你有更多的出生日期时,找到一个和另一个生日相同的人的可能性就会增加,而两个人的生日可能是一样的。最终你会找到一个过同样生日的人。
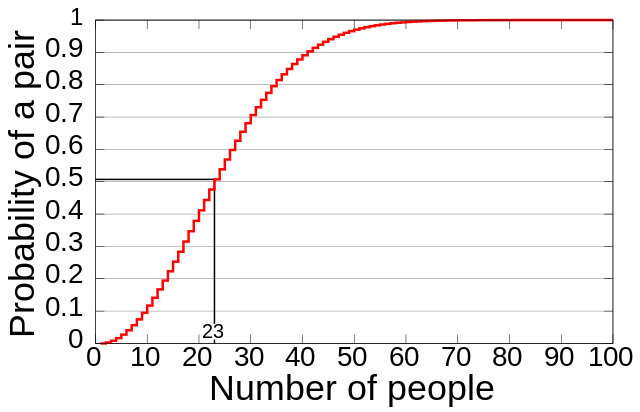
亚伦·托彭在他的文章““SHA1的现实””中提到了这一点,他指出:
SHA1本来是要取代MD5的。MD5的输出空间只有128位,其中SHA1的输出空间为160位。SHA1的设计也不同于MD5,其目的是避免MD5所面临的相同类型的弱点或攻击。然而,随着时间的推移,密码学家已经能够对SHA1进行严重的攻击,因此,他们都警告我们不要使用SHA1,转而使用SHA2。应该需要2160个操作才能找到与SHA1的冲突,但是使用生日悖论,在大约2^80个操作中发现SHA1碰撞的概率可以达到50%。然而,密码分析人员已经将SHA1的复杂度降低到了2^61操作。甚至更好。
从本质上说,SHA1是一种数学算法,在算法中可以发现其弱点,使其更容易开裂,降低碰撞概率。这一研究通常由计算机科学家、密码学家和数学家完成,通过使用新的算法寻找新的碰撞方法,可以减少发现碰撞的机会。
https://stackoverflow.com/questions/22390427
复制相似问题

