numpy中的二阶梯度
我试着用数值计算numpy中数组的二阶梯度。
a = np.sin(np.arange(0, 10, .01))
da = np.gradient(a)
dda = np.gradient(da)这就是我想出来的。是否应该这样做呢?
我问这个问题,因为在numpy中没有一个选项是np.gradient(a,order=2)。我担心这种用法是否错误,这就是numpy没有实现这一点的原因。
PS1:我知道有np.diff(a,2)。但是这只是片面的估计,所以我很好奇为什么np.gradient没有类似的关键字。
PS2: np.sin()是一个玩具数据--真正的数据没有解析形式。
谢谢!
回答 6
Stack Overflow用户
发布于 2014-05-02 01:35:00
数值梯度计算没有通用的正确答案。在计算样本数据的梯度之前,您必须对生成该数据的底层函数做一些假设。您可以在技术上使用np.diff进行梯度计算。使用np.gradient是一种合理的方法。我看不出你在做什么,这是一维函数的二阶导数的一个特别的近似。
Stack Overflow用户
发布于 2014-05-02 14:49:04
我将第二句@jrennie的第一句话--这一切都取决于此。numpy.gradient函数要求数据间隔均匀(如果多维,则允许在每个方向上的不同距离)。如果您的数据不遵守这一点,那么numpy.gradient就不会有多大用处。实验数据可能有(好的,将有)噪音,除了不一定都是均匀的间隔。在这种情况下,最好使用scipy.interpolate样条函数(或对象)之一。它们可以接受不均匀的数据,允许平滑,并且可以将导数返回到k-1,其中k是样条拟合的顺序。K的默认值是3,所以二阶导数很好。示例:
spl = scipy.interpolate.splrep(x,y,k=3) # no smoothing, 3rd order spline
ddy = scipy.interpolate.splev(x,spl,der=2) # use those knots to get second derivative 像scipy.interpolate.UnivariateSpline这样的面向对象样条有衍生产品的方法。注意,派生方法是在Sciy0.13中实现的,而在0.12中不存在。
请注意,正如@JosephCottham在2018年的评论中指出的那样,这个答案(至少适合Numpy 1.08 )不再适用,因为(至少) Numpy 1.14。检查您的版本号和可用的呼叫选项。
Stack Overflow用户
发布于 2020-02-24 16:37:48
对于一阶导数中的不连续性,双梯度法失败。由于梯度函数将一个数据点放在左边和右边,这在多次应用时会继续/扩展。
另一方面,二阶导数可以用公式来计算。
d^2 f(x[i]) / dx^2 = (f(x[i-1]) - 2*f(x[i]) + f(x[i+1])) / h^2比较这里。这样做的好处是只考虑两个相邻的像素。
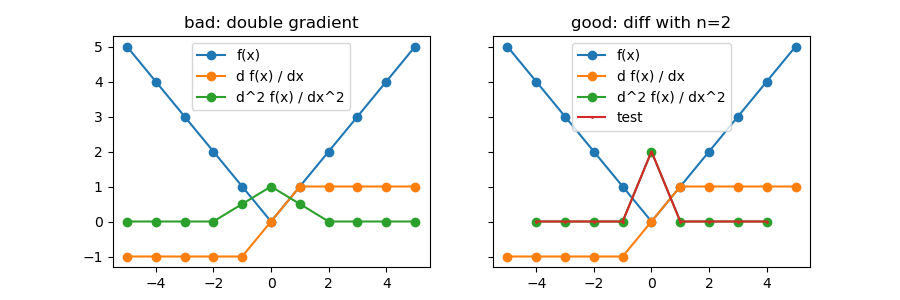
在图中,比较了由np.gradient实现的双np.diff方法(左)和上述公式(右)。由于f(x)在零点只有一个扭结,那么二阶导数(绿色)应该只有一个峰值。当双梯度解在每个方向上考虑两个相邻点时,导致在+/- 1处存在有限的二阶导数值。
然而,在某些情况下,您可能希望采用双梯度解,因为这对噪声更有鲁棒性。
我不知道为什么会有np.gradient和np.diff,但原因可能是,np.gradient的第二个参数定义了像素距离(对于每个维度),对于图像,它可以同时应用于两个维度-- gy, gx = np.gradient(a)。
码
import numpy as np
import matplotlib.pyplot as plt
xs = np.arange(-5,6,1)
f = np.abs(xs)
f_x = np.gradient(f)
f_xx_bad = np.gradient(f_x)
f_xx_good = np.diff(f, 2)
test = f[:-2] - 2* f[1:-1] + f[2:]
# lets plot all this
fig, axs = plt.subplots(1, 2, figsize=(9, 3), sharey=True)
ax = axs[0]
ax.set_title('bad: double gradient')
ax.plot(xs, f, marker='o', label='f(x)')
ax.plot(xs, f_x, marker='o', label='d f(x) / dx')
ax.plot(xs, f_xx_bad, marker='o', label='d^2 f(x) / dx^2')
ax.legend()
ax = axs[1]
ax.set_title('good: diff with n=2')
ax.plot(xs, f, marker='o', label='f(x)')
ax.plot(xs, f_x, marker='o', label='d f(x) / dx')
ax.plot(xs[1:-1], f_xx_good, marker='o', label='d^2 f(x) / dx^2')
ax.plot(xs[1:-1], test, marker='o', label='test', markersize=1)
ax.legend()https://stackoverflow.com/questions/23419193
复制相似问题

