用FFT算法计算
用FFT算法计算
提问于 2014-05-13 09:40:55
给出一组n粒子电荷载流子在点(1,0),(2,0),.(n,0)飞机上。在点(i,0)中发现的粒子电荷称为气。作用在粒子上的力由公式给出:
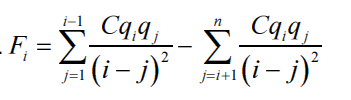
C是库仑常数。
给出了计算所有粒子在总复杂度O(nlgn)中计算Fi的算法。提示:使用FFT算法。
似乎菲已经被划分为偶数和奇点。
我想把每个和除以计算FFT (但是除以到..?)然后,和所有点的一半(因为这是FFT引起的),然后减去公式上给出的和的结果。
知道如何做得更好吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2014-05-13 10:44:35
看起来像家庭作业,所以没有为您的案例提供实际的代码,而是提供一些示例和提示。
对于FFT-like算法:
2通过零填充将数据集大小设置为的幂。 因此,对一半的划分很简单(没有残余物)。- 创建递归函数来计算类似FFT的内容。
在它中,重新排序数据集,将其分成两半,递归地称它为self 2次(每一次使用不同的一半数据),并添加if语句开始。如果dataset
size<=1或2,则直接返回计算值,以确保递归停止。 在这两个递归调用之后,将数据重新排序,并将它们组合起来以得到结果。 - 如果需要的话,从结果中删除零填充
例如,这就是我的NTT的样子(数论转换)。
//---------------------------------------------------------------------------
void fourier_NTT:: NTT_fast(DWORD *dst,DWORD *src,DWORD n,DWORD w)
{
// recursion stop condition if the data is single number ...
if (n<=1) { if (n==1) dst[0]=src[0]; return; }
DWORD i,j,a0,a1,n2=n>>1,w2=modmul(w,w);
// reorder even,odd to dst array
for (i=0,j=0;i<n2;i++,j+=2) dst[i]=src[j];
for ( j=1;i<n ;i++,j+=2) dst[i]=src[j];
// recursion
NTT_fast(src ,dst ,n2,w2); // even
NTT_fast(src+n2,dst+n2,n2,w2); // odd
// restore results
for (w2=1,i=0,j=n2;i<n2;i++,j++,w2=modmul(w2,w))
{
a0=src[i];
a1=modmul(src[j],w2);
dst[i]=modadd(a0,a1);
dst[j]=modsub(a0,a1);
}
}
//---------------------------------------------------------------------------完整的源代码和更多的信息是here。
总是比较快速实现结果和慢实现!!
随着数据集大小的增长,某些系数或索引中的小误差可能会导致结果的巨大差异。
对于上述NTT函数,这是缓慢的实现:
//---------------------------------------------------------------------------
void fourier_NTT:: NTT_slow(DWORD *dst,DWORD *src,DWORD n,DWORD w)
{
DWORD i,j,wj,wi,a,n2=n>>1;
for (wj=1,j=0;j<n;j++)
{
a=0;
for (wi=1,i=0;i<n;i++)
{
a=modadd(a,modmul(wi,src[i]));
wi=modmul(wi,wj);
}
dst[j]=a;
wj=modmul(wj,w);
}
}
//---------------------------------------------------------------------------Notes
- 现在你有了分离方程 导出直接计算值与由2x半递归调用计算的值之间的系数差,并相应地恢复结果,从而使输出与正确的结果相匹配。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/23627751
复制相关文章
相似问题

