利用SciPy的gaussian_kde函数获取带宽
我使用SciPy的kde函数从x,y点的数据集生成一个核密度估计(kde)函数。
这是我的代码的一个简单的MWE:
import numpy as np
from scipy import stats
def random_data(N):
# Generate some random data.
return np.random.uniform(0., 10., N)
# Data lists.
x_data = random_data(100)
y_data = random_data(100)
# Obtain the gaussian kernel.
kernel = stats.gaussian_kde(np.vstack([x_data, y_data]))由于我没有手动设置带宽(通过bw_method键),函数默认使用Scott规则(请参阅函数的描述)。我需要的是通过stats.gaussian_kde函数自动获得这个带宽值。
我试过用:
print kernel.set_bandwidth()但是它总是返回None而不是浮点。
回答 3
Stack Overflow用户
发布于 2016-03-08 17:55:28
短答案
带宽是kernel.covariance_factor() 乘以您正在使用的示例的std。
(这是在1D样本的情况下,在默认情况下使用Scott的经验法则计算)。
示例:
from scipy.stats import gaussian_kde
sample = np.random.normal(0., 2., 100)
kde = gaussian_kde(sample)
f = kde.covariance_factor()
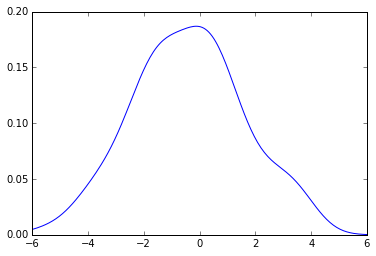
bw = f * sample.std()你得到的pdf是:
from pylab import plot
x_grid = np.linspace(-6, 6, 200)
plot(x_grid, kde.evaluate(x_grid))
您可以这样检查它,如果您使用一个新的函数来创建一个kde,比如说使用sklearn:
from sklearn.neighbors import KernelDensity
def kde_sklearn(x, x_grid, bandwidth):
kde_skl = KernelDensity(bandwidth=bandwidth)
kde_skl.fit(x[:, np.newaxis])
# score_samples() returns the log-likelihood of the samples
log_pdf = kde_skl.score_samples(x_grid[:, np.newaxis])
pdf = np.exp(log_pdf)
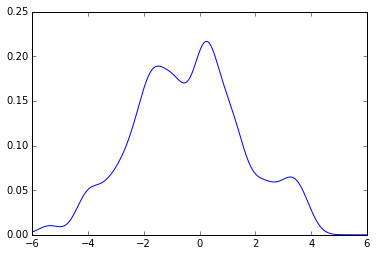
return pdf现在,使用上面的相同代码,您可以得到:
plot(x_grid, kde_sklearn(sample, x_grid, f))
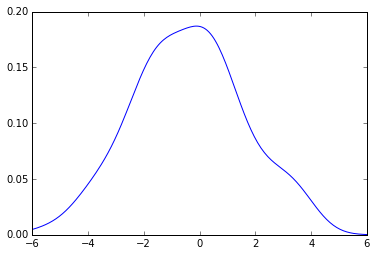
plot(x_grid, kde_sklearn(sample, x_grid, bw))
Stack Overflow用户
发布于 2014-05-13 12:12:16
我明白了,台词是:
kernel.covariance_factor()来自因子
计算乘以数据协方差矩阵得到核协方差矩阵的系数(kde.factor)。默认情况是因子。子类可以覆盖此方法以提供不同的方法,或者通过调用kde.set_bandwidth来设置它。
可以检查使用此带宽值生成的内核是否等效于使用默认带宽生成的内核。为此,获得一个具有covariance_factor()提供的带宽的新内核,并将其在随机点上的值与原始内核进行比较:
kernel = stats.gaussian_kde(np.vstack([x_data, y_data]))
print kernel([0.5, 1.3])
bw = kernel.covariance_factor()
kernel2 = stats.gaussian_kde(np.vstack([x_data, y_data]), bw_method=bw)
print kernel2([0.5, 1.3])Stack Overflow用户
发布于 2018-12-31 12:05:09
我遇到了一个老问题,因为我还想知道gaussian_kde使用的带宽是多少。我想添加/修正以前的答案,即协方差因子在kde.py代码中使用,如: self.covariance = self._data_covariance * self.factor**2
因此,完整的内核协方差是样本协方差乘以所谓的协方差因子(Scott )的平方,可以由kde.factor或kde.covariance_factor()检索。
https://stackoverflow.com/questions/23630515
复制相似问题

