问Jacobi迭代没有结束

EN

你的代码是正确的。它似乎不起作用的原因是，当您使用Jacobi迭代时，您指定的是可能不会收敛的系统。

具体来说(感谢@Saraubh)，如果矩阵A是严格意义上的 对角占优，则此方法将收敛。换句话说，对于矩阵中的每一行i，i行中所有列j的绝对求和不带i的对角线系数，必须是小于，而不是对角线本身。换言之：

​

​

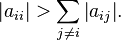
但是，有些系统将与Jacobi收敛，即使这个条件不满足，但在尝试为您的系统使用Jacobi之前，应该将其作为一般规则使用。如果你使用Gauss，它实际上更稳定。唯一的区别是，您正在重复使用x的解决方案，并在沿行前进时将其输入其他变量。要使这个Gauss，您所要做的就是改变您的for循环中的一个字符。将其更改为：

xp(i) = 1/A(i,i)*(b(i) - A(i,1:i-1)*x(1:i-1) - A(i,i+1:n)*x(i+1:n));

对此：

xp(i) = 1/A(i,i)*(b(i) - A(i,1:i-1)*xp(1:i-1) - A(i,i+1:n)*x(i+1:n));
                                    **HERE**

下面是两个示例，我将向您展示：

1. 其中我们指定了一个不被Jacobi收敛的系统，但是有一个解决方案。这个系统是，而不是对角线占优势。
2. 其中我们指定了一个确实由Jacobi收敛的系统。具体来说，这个系统是对角占优势的。

示例1

A = [1 2 2 3; -1 4 2 7; 3 1 6 0; 1 0 3 4];
b = [0;1;-1;2];
x = Jacobi(A, b, 0.001, 40)
xtrue = A \ b

x =

1.0e+09 *

4.1567
0.8382
1.2380
1.0983

xtrue =

-0.1979
-0.7187
 0.0521
 0.5104

现在，如果我使用Gauss解，我得到的是：

x =

-0.1988
-0.7190
0.0526
0.5103

哇！它收敛于Gauss，而不是Jacobi，即使系统不是对角占优，我可能对此有一个解释，稍后我会给出解释。

例2

A = [10 -1 2 0; -1 -11 -1 3; 2 -1 10 -1; 0 3 -1 8];
b = [6;25;-11;15];
x = Jacobi(A, b, 0.001, 40);
xtrue = A \ b

x =

0.6729
-1.5936
-1.1612
2.3275

xtrue =

0.6729
-1.5936
-1.1612
2.3274

这就是我对高斯-塞德尔的看法：

x =

0.6729
-1.5936
-1.1612
2.3274

这两者都是一致的，而且这个系统是对角占优势的。

因此，您的代码没有任何错误。您只是指定了一个无法使用Jacobi解决的系统。最好是用Gauss迭代法来解决这类问题。之所以如此，是因为您正在立即使用来自当前迭代的信息，并将其扩展到其他变量。雅各比没有这么做，这就是为什么它会更快地发散的原因。对于Jacobi，您可以看到示例1未能收敛，而示例2却收敛了。Gauss对两者都进行了会聚。事实上，当它们都汇聚在一起时，它们很接近真正的解决方案。

同样，您需要确保您的系统是对角占优势的，以便保证您的系统具有收敛性。不执行这个规则..。好吧..。你将承担一个风险，因为它可能会或可能不会收敛。

祝好运!

虽然这并没有指出代码中的问题，但我相信您正在寻找数值方法: Jacobi文件交换提交。

%JACOBI   Jacobi iteration for solving a linear system.
% Sample call
%   [X,dX] = jacobi(A,B,P,delta,max1)
%   [X,dX,Z] = jacobi(A,B,P,delta,max1)

它看起来就像你描述的那样。

正如其他人指出的那样，并不是所有的系统都是用Jacobi方法收敛的，但它们没有指出原因？实际上，只有一小部分子系统与Jacobi方法相收敛。

收敛准则是，“一列中所有系数(非对角线)之和”必须小于“该行对角线位置上的系数”。所有行都必须满足此标准。您可以在以下网址阅读更多内容：Jacobi方法收敛性

在决定使用Jacobi方法之前，必须先看看这个准则是否符合数值方法。Gauss方法有一个稍微宽松的收敛准则，它允许你在大多数有限差分型数值方法中使用它。