实对称向量的FFT不是实的和对称的
我很难理解什么应该是一个简单的概念。我在MATLAB中构造了一个向量,它是实的和对称的。当我在MATLAB中使用FFT时,得到的结果有一个重要的虚分量,尽管傅里叶变换的对称规则说,实对称函数的FT也应该是实的和对称的。我的示例代码:
N = 1 + 2^8;
k = linspace(-1,1,N);
V = exp(-abs(k));
Vf1 = fft(fftshift(V));
Vf2 = fft(ifftshift(V));
Vf3 = ifft(fftshift(V));
Vf4 = ifft(ifftshift(V));
Vf5 = fft(V);
Vf6 = ifft(V);
disp([isreal(Vf1) isreal(Vf2) isreal(Vf3) isreal(Vf4) isreal(Vf5) isreal(Vf6)])结果:
0 0 0 0 0 0(i)fft或(i)fftshift的任何组合都不会产生真正的对称向量。我尝试过偶数和奇数N (N = 2^8 vs. N = 1+2^8)。
我试着看了一下k+flip(k),在eps(1)的数量级上有一些残差,但是残差也是对称的,并且at的虚部不是eps(1)数量级上的模糊,而是与真实部分相当的大小。
我错过了什么显而易见的东西?
,我错过了一件显而易见的事情:
FFT不是在所有空间上的积分,所以它假定一个周期信号。上面,我重复了我选择偶数N期间的最后一点,所以没有办法将零频率移到零频率,而没有分数索引,这是不存在的。
关于我选择k的事。这不是武断的。我试图解决的实际问题是生成一个模型FTIR干涉图,然后我将FFT得到一个光谱。k是干涉仪移动的距离,它在波本子中转换为频率。在实际问题中,会有各种尺度因子,因此生成函数V将产生物理上有意义的数字。
回答 4
Stack Overflow用户
发布于 2014-07-31 10:14:05
@Yvon关于对称性的评论是完全正确的。您的输入信号看起来是对称的,但并不是因为对称性与原点0有关。在Matlab中使用线性空间来构造信号是一个很糟糕的选择。试图用fftshift来修复结果也是个坏主意。
改为使用:
k = 2*(0:N-1)/N - 1;你就会得到你想要的结果。然而,变换后的值的虚部不会完全为零。有一些数字噪音。
>> max(abs(imag(Vf5)))
ans =
2.5535e-15对Yvon问题的回答:
为什么?>> N= 1+2^4 N= 17 >> x=linspace(-1,1,( N) x= -1.0000 -0.8750 -0.7500 -0.6250 -0.5000 -0.3750 -0.2500 -0.1250 0 0.1250 0.2500 0.3750 0.5000 0.6250 0.7500 0.8750 1.0000 >> y=2*(0:N-1)/N-1 y= -1.0000 -0.8824-0.7647 -0.6471-0.5294 -0.4118 -0.2941 -0.1765 -0.0588 0.0588 0.1765 0.2941 0.4118 0.5294 0.6471 0.7647 0.8824-Yvon 1
您的示例不是对称(偶数)函数,而是反对对称(奇数)函数。然而,这并没有什么不同。
对于长度为N的反对称函数,下列语句为真:
f[i] == -f[-i] == -f[N-i]我的索引从0到N1。
让我们看看i=2发生了什么。记住,计数以0开头,以16结尾。
x[2] = -0.75
-x[N-2] == -x[17-2] == -x[15] = (-1) 0.875 = -0.875
x[2] != -x[N-2]
y[2] = -0.7647
-y[N-2] == -y[15] = (-1) 0.7647
y[2] == y[N-2]问题是,Matlab向量的原点从1开始,模(周期)向量从原点0开始。这种差异导致了许多误解。
解释linspace(-1,+1,N)不正确的另一种方法:
假设你有一个向量,它包含一个周期函数的单个周期,例如,一个Cosinus函数。这一个周期是无限多个周期之一。您的Cosinus向量的第一个值不能与您的向量的最后值相同。然而,这正是linspace(-1,+1,N)所做的。这样做,会产生一个序列,其中周期1的最后一个值与下一个句点2的第一个示例值相同。这不是您想要的结果。为避免这一错误,请使用t= 2*(0:N-1)/N - 1。距离ti+1-ti为2/N,最后的值必须是tN-1 = 1 - 2/N,而不是1。
对Yvon第二个评论的回答
无论你在DFT/FFT的输入向量中放入什么,理论上它都被解释为一个周期函数。但这不是重点。
DFT执行一个集成。
fft(m) = Sum_(k=0)^(N-1) (x(k) exp(-i 2 pi m k/N )第一值x(k=0)描述长度1/N的第一积分间隔的幅度,第二值x(k=1)描述长度1/N的第二积分间隔的幅度,等等。
对称函数的最后一个积分区间以与第一个示例相同的值结束。这意味着,最后一个积分区间的起点是k=N1= 1-1/N,您的输入向量持有积分区间的起点。
因此,对称k=N的最后一点是函数的一个点,但它不是积分区间的起点,因此它不是输入向量的一个成员。
Stack Overflow用户
发布于 2014-07-30 16:56:15
它是
Vf = fftshift(fft(ifftshift(V)));也就是说,在时域需要ifftshift,这样样本被解释为对称函数的样本,然后在频域的fftshift使对称性变得明显。
这只适用于N奇数。甚至对N来说,对称函数的概念是没有意义的:没有办法使信号相对于原点是对称的(起源需要“两个样本之间”,这是不可能的)。
对于您的示例V,上面的代码给出了真实的和对称的Vf。下面的图是用semilogy(Vf)生成的,这样就可以看到小值和大值。(当然,您可以修改水平轴,使图形按其应有的频率以0为中心;但无论如何,图形是对称的。)
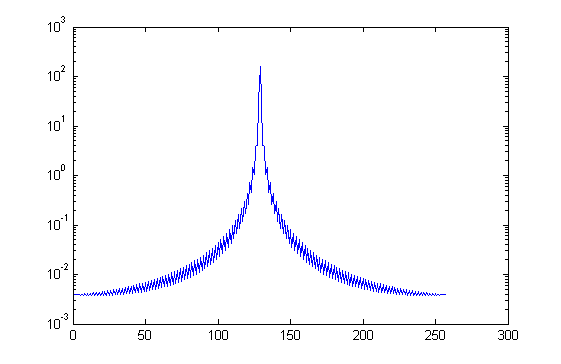
Stack Overflow用户
发布于 2014-07-30 17:17:43
您在实现“对称”概念时遇到了问题。纯实,偶数(或“对称”)函数有一个傅里叶变换函数,它也是实的和偶数的。“偶数”是关于y轴或t=0线的对称性。
然而,在Matlab中实现信号时,您总是从t=0开始。也就是说,没有办法“定义”从时间起源之前开始的信号。
在互联网上搜索一段时间后,我会找到这个-- 在fft和ifft输入端正确使用fftshift和ifftshift。
就像Luis有指出一样,您需要在将信号输入fft之前执行ifftshift。这个原因从来没有在Matlab中被记录过,只是在这个线程中。由于历史原因,交换了fft和ifft的输出和输入。也就是说,不是从-N/2排序到N/2-1 (自然顺序),而是将时域或频域信号从0排序到N/2-1,然后从-N/2排序到-1。这意味着,正确的编码方式是fft( ifftshift(V) ),,但大多数人在大多数情况下忽略了。为什么它被默默地忽略,而不是引起巨大的问题,最关心的是信号的振幅,而不是相位。由于圆形移位不影响振幅谱,这并不是一个问题(即使是Matlab的人谁写了文件)。
为了检查振幅相等-
Vf2 = fft(ifftshift(V));
Vf5 = fft(V);
Va2 = abs(fftshift(Vf2));
Va5 = abs(fftshift(Vf5));
>> min(abs(Va2-Va5)<1e-10)
ans =
1看看这段时间有多糟糕-
Vp2 = angle(fftshift(Vf2));
Vp5 = angle(fftshift(Vf5));不管怎么说,正如我在评论中所写的,在将代码复制并粘贴到一个新鲜干净的Matlab中之后,它会给出0 1 0 1 0 0。
对于关于N=even和N=odd的问题,我的观点是,当N=even时,信号是不对称的,因为在时间起源的两边都有不相等的点数。
https://stackoverflow.com/questions/25042379
复制相似问题

