提取由matplotlib补丁包围的坐标。
提取由matplotlib补丁包围的坐标。
提问于 2014-08-05 18:32:04
我使用matplotlib.patches.ellipse创建了一个椭圆,如下所示:
patch = mpatches.Ellipse(center, major_ax, minor_ax, angle_deg, fc='none', ls='solid', ec='g', lw='3.')我想要的是包含在这个补丁中的所有整数坐标的列表。也就是说,如果我要把这个椭圆和同一个网格上的每一个整数点一起画出来,那么这些点中有多少在椭圆中呢?
我试着看我是否能提取椭圆的方程,这样我就可以遍历每一个点,看看它是否在直线内,但我似乎找不到一个明显的方法来做到这一点,它变得更加复杂,因为椭圆的主轴可以在任意角度上定位。这样做的信息必须存储在某个地方的补丁中,但我似乎找不到它。
如对此有任何建议,将不胜感激。
Stack Overflow用户
发布于 2014-08-05 22:50:44
如果您真的想使用matplotlib提供的方法,那么:
import matplotlib.pyplot as plt
import matplotlib.patches
import numpy as np
# create an ellipse
el = matplotlib.patches.Ellipse((50,-23), 10, 13.7, 30, facecolor=(1,0,0,.2), edgecolor='none')
# find the bounding box of the ellipse
bb = el.get_window_extent()
# calculate the x and y points possibly within the ellipse
x_int = np.arange(np.ceil(bb.x0), np.floor(bb.x1) + 1, dtype='int')
y_int = np.arange(np.ceil(bb.y0), np.floor(bb.y1) + 1, dtype='int')
# create a list of possible coordinates
g = np.meshgrid(x_int, y_int)
coords = np.array(zip(*(c.flat for c in g)))
# create a list of transformed points (transformed so that the ellipse is a unit circle)
transcoords = el.get_transform().inverted().transform(coords)
# find the transformed coordinates which are within a unit circle
validcoords = transcoords[:,0]**2 + transcoords[:,1]**2 < 1.0
# create the list of valid coordinates (from untransformed)
ellipsepoints = coords[validcoords]
# just to see if this works
fig = plt.figure()
ax = fig.add_subplot(111)
ax.add_artist(el)
ep = np.array(ellipsepoints)
ax.plot(ellipsepoints[:,0], ellipsepoints[:,1], 'ko')似乎奏效了:
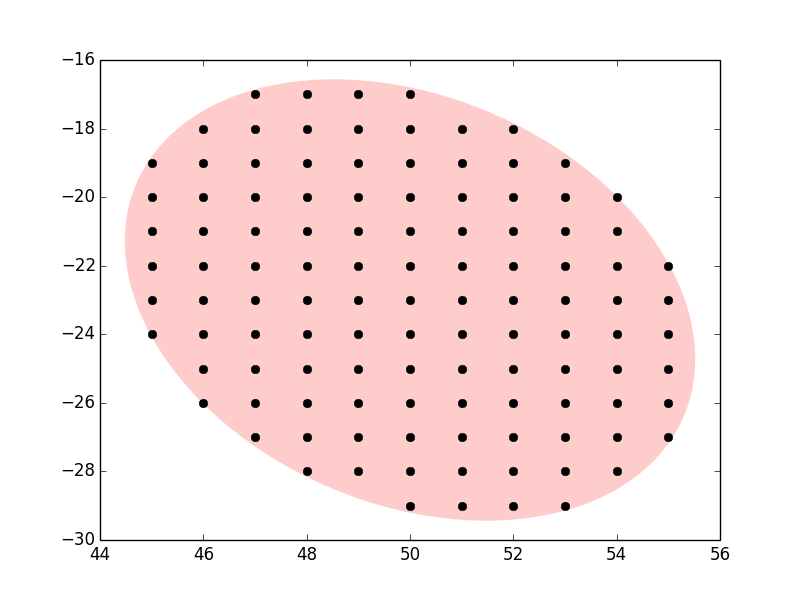
(放大显示,就连挂在边缘的点也在里面。)
这里的要点是,matplotlib将椭圆处理为转换的圆(平移、旋转、缩放,任何仿射)。如果逆变换,则结果是原点的单位圆,检验点是否在原点内是非常简单的。
只是一个警告:get_window_extent可能不是非常可靠,因为它似乎使用了一个圆的样条近似。另外,请参阅tcaswell对呈现器依赖项的评论。
为了找到一个更可靠的包围盒,你可以:
- 在地块坐标中创建水平和垂直向量(它们的位置不重要,(0,0,1,0)和(0,0,0,1)就可以了)
- 将这些矢量转换为椭圆坐标(
get_transform等) - 在椭圆坐标系(即椭圆是原点周围的单位圆的系统)中,找到与这两个矢量平行的圆的四个切线。
- 找到向量的交点(4个交叉口,但2个对角线就足够了)
- 将交点转换回地块坐标
这将提供一个精确的(但当然受到数值精度的限制)的方形包围盒。
但是,您可以使用一个简单的近似:
- 所有可能的点都在一个圆内,其中心与椭圆的中心相同,其直径与椭圆的主轴直径相同。
换句话说,所有可能的点都在x0+-m/2,y0+-m/2之间的方框内,其中(x0,y0)是椭圆的中心,m是主轴。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/25145931
复制相关文章
相似问题

