宽度优先搜索效率
在无界/无限国际象棋棋盘上,计算从x1、y1到x2、y2所需的最少跳数,最有效的方法是什么?假设从x1,y1,我们总是可以生成一组合法的动作。
这听起来是为BFS量身定做的,我已经成功地实现了一个。但是如果x2,y2是任意大的话,它的空间和时间复杂性似乎是非常可怕的。
我一直在研究其他各种算法,如A*、双向搜索、迭代深化DFS等,但到目前为止,我还不知道哪种方法会产生最优(和最完整)的解决方案。有没有什么我缺少的洞察力?
回答 3
Stack Overflow用户
发布于 2014-08-11 12:45:47
为了扩展评论中的讨论,像宽度优先搜索(BFS)这样的不知情搜索将找到最优解(最短路径)。然而,它只考虑到到目前为止节点g(n)的成本,并且它的成本随着从源到目标的距离呈指数增长。为了驯服搜索的成本,同时仍然确保搜索找到最优的解决方案,您需要通过启发式的h(n)将一些信息添加到搜索算法中。
您的情况非常适合A*搜索,其中启发式是从节点到目标(x2,y2)距离的度量。你可以用欧几里得距离“就像乌鸦飞”,但是当你在考虑骑士的时候,曼哈顿的距离可能更合适。无论您选择什么度量,它必须小于(或等于)从节点到目标的实际距离,以便搜索到最优解(在这种情况下,启发式被称为“可接受”)。请注意,您需要将每个距离除以一个常数,以使其低估移动:曼哈顿距离除以3,欧几里得距离除以sqrt(5) (sqrt(5)是2乘1平方的对角线长度)。
当您运行该算法时,您将估计来自我们已经到达的任何节点的f(n)的总距离,即到目前为止的距离加上启发式距离。即f(n) = g(n) + h(n),g(n)是从(x1,y1)到节点n的距离,h(n)是从节点n到(x2,y2)的估计启发式距离。给定您需要的节点,您总是选择f(n)最低的节点f(n)。我喜欢你的说法:
维护一个由
g(n) + h(n)命令签出的节点优先级队列。
如果启发式是可接受的,则该算法找到最优解,因为次优路径永远不可能位于优先级队列的前面:最优路径的任何片段总距离总是较低的(其中,总距离是产生距离加启发式距离)。
我们在这里选择的距离度量是单调的(即,随着路径的延长而不是向上或向下增加)。在这种情况下,可以证明它是有效的。如往常一样,请参阅维基百科或网络上的其他来源以获得更多详细信息。科罗拉多州立大学网页特别好,并且对最优性和效率进行了很好的讨论。
举一个从(-200,-100)到(0,0)的例子,这相当于(0,0)到(200,100)的例子,在我的实现中,我们看到的曼哈顿启发式如下
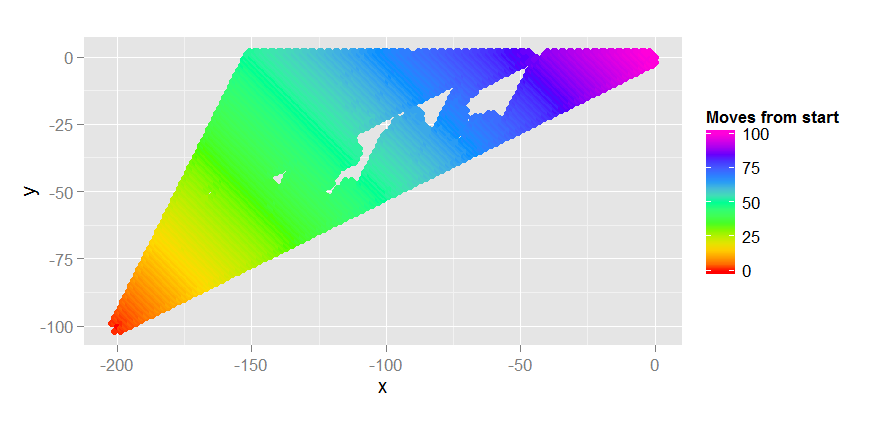
该实现进行了过多的搜索,因为使用启发式的h =曼哈顿距离,跨1向上2的步骤似乎与跨2向上1的最佳步骤一样好,即f()值没有区分两者。然而,该算法仍能找到100次移动的最优解。它需要2118个步骤,这仍然比广度优先搜索要好得多,后者像墨迹一样扩散开来(我估计它可能需要20000到30000步)。
如果你选择h =欧几里得距离,它是怎么做的?
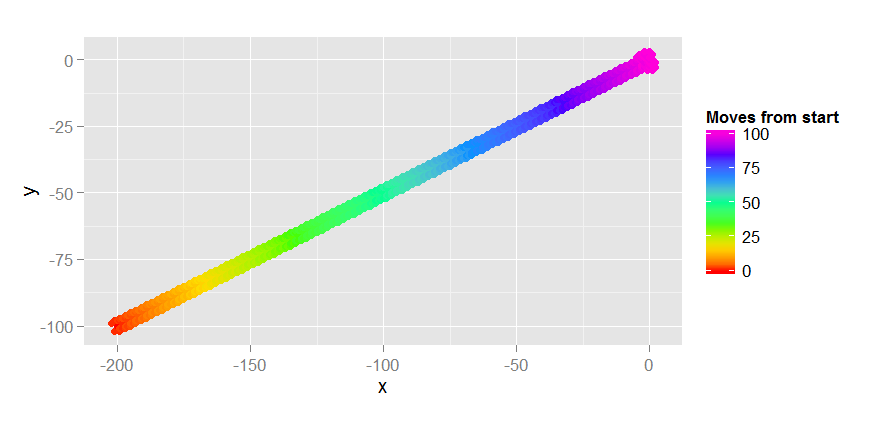
这好多了!它只需要104步,而且它做得很好,因为它结合了我们的直觉,你需要向大致正确的方向前进。但是在我们祝贺自己之前,让我们尝试另一个例子,从(-200,0)到(0,0)。这两种启发式方法都可以找到长度为100的最佳路径。欧几里得启发式需要12171步来寻找最优路径,如下所示。
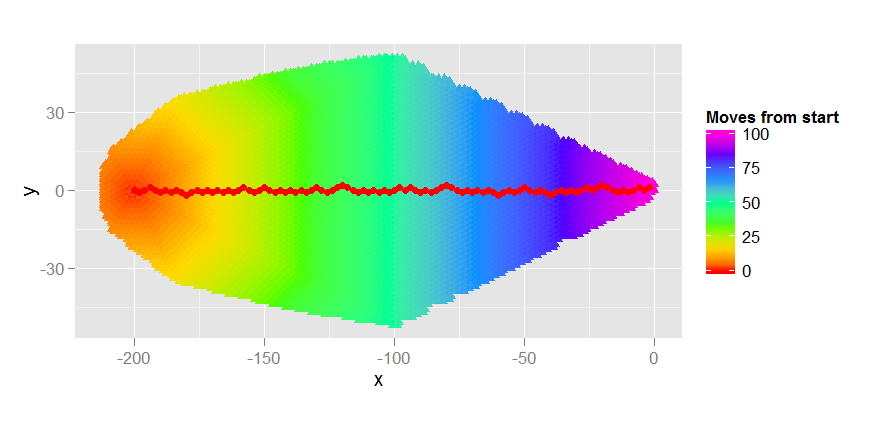
而曼哈顿的启发式则要走16077步

抛开曼哈顿的启发式更糟糕的事实相比,我认为真正的问题是有多条最优路径。这并不奇怪:最优路径的重新排序仍然是最优的。通过按照@Sneftel的答案以数学形式重新处理这个问题,这一事实就会自动得到考虑。
总之,与BFS相比,具有容许启发式的A*产生的最优解比BFS更有效,但很可能存在更有效的解。A*是一种很好的默认算法,在这种情况下,您可以很容易地找到一个距离启发式算法,虽然在这种情况下,它并不是最好的解决方案,但是通过实现它可以了解很多关于这个问题的知识。
请按您的要求在C++中编写下面的代码。
#include <memory>
using std::shared_ptr;
#include <vector>
using std::vector;
#include <queue>
using std::priority_queue;
#include <map>
using std::map;
using std::pair;
#include <math.h>
#include <iostream>
using std::cout;
#include <fstream>
using std::ofstream;
struct Point
{
short x;
short y;
Point(short _x, short _y) { x = _x; y = _y; }
bool IsOrigin() { return x == 0 && y == 0; }
bool operator<(const Point& p) const {
return pair<short, short>(x, y) < pair<short, short>(p.x, p.y);
}
};
class Path
{
Point m_end;
shared_ptr<Path> m_prev;
int m_length; // cached
public:
Path(const Point& start)
: m_end(start)
{ m_length = 0; }
Path(const Point& start, shared_ptr<Path> prev)
: m_end(start)
, m_prev(prev)
{ m_length = m_prev->m_length +1; }
Point GetEnd() const { return m_end; }
int GetLength() const { return m_length; }
vector<Point> GetPoints() const
{
vector<Point> points;
for (const Path* curr = this; curr; curr = curr->m_prev.get()) {
points.push_back(curr->m_end);
}
return points;
}
double g() const { return m_length; }
//double h() const { return (abs(m_end.x) + abs(m_end.y)) / 3.0; } // Manhattan
double h() const { return sqrt((m_end.x*m_end.x + m_end.y*m_end.y)/5); } // Euclidian
double f() const { return g() + h(); }
};
bool operator<(const shared_ptr<Path>& p1, const shared_ptr<Path>& p2)
{
return 1/p1->f() < 1/p2->f(); // priority_queue has biggest at end of queue
}
int main()
{
const Point source(-200, 0);
const Point target(0, 0);
priority_queue<shared_ptr<Path>> q;
q.push(shared_ptr<Path>(new Path(source)));
map<Point, short> endPath2PathLength;
endPath2PathLength.insert(map<Point, short>::value_type(source, 0));
int pointsExpanded = 0;
shared_ptr<Path> path;
while (!(path = q.top())->GetEnd().IsOrigin())
{
q.pop();
const short newLength = path->GetLength() + 1;
for (short dx = -2; dx <= 2; ++dx){
for (short dy = -2; dy <= 2; ++dy){
if (abs(dx) + abs(dy) == 3){
const Point newEnd(path->GetEnd().x + dx, path->GetEnd().y + dy);
auto existingEndPath = endPath2PathLength.find(newEnd);
if (existingEndPath == endPath2PathLength.end() ||
existingEndPath->second > newLength) {
q.push(shared_ptr<Path>(new Path(newEnd, path)));
endPath2PathLength[newEnd] = newLength;
}
}
}
}
pointsExpanded++;
}
cout<< "Path length " << path->GetLength()
<< " (points expanded = " << pointsExpanded << ")\n";
ofstream fout("Points.csv");
for (auto i : endPath2PathLength) {
fout << i.first.x << "," << i.first.y << "," << i.second << "\n";
}
vector<Point> points = path->GetPoints();
ofstream fout2("OptimalPoints.csv");
for (auto i : points) {
fout2 << i.x << "," << i.y << "\n";
}
return 0;
}注意,这不是很好的测试,所以很可能会有but,但我希望总体思路是明确的。
Stack Overflow用户
发布于 2014-08-11 04:10:15
我还没有一个完整的证据,但我相信,如果x1,y1和x2,y2在两个方向上都很遥远,那么任何最优的解决方案都会有许多直接向x2和直接向y2移动的移动(2种可能的L型移动,向这个方向移动)。例如,如果当前位置x接近x2,但当前位置y远离y2,则在向y2移动两个方格的两个移动之间交替进行。类似地,如果y接近y2,那么x和x2是很远的。然后,只要到x2的垂直距离和水平距离都小于一些相当小的阈值(可能是5或10),那么就必须用BFS或其他方法来解决问题,才能得到最优解,并且您得到的解应该是最优的。当我有证据时,我会更新我的答案,但我几乎肯定这是真的。如果是这样的话,这意味着无论x1、y1和x2之间有多远,基本上只要解决水平和垂直距离为5或10的问题,就可以快速完成。
Stack Overflow用户
发布于 2014-08-11 13:04:43
如果合法移动集独立于当前空间,那么作为整数线性规划(ILP)问题,这似乎是理想的。您基本上可以解决每种类型移动的数量,这样移动的总数就会最小化。例如,对于被限制只能向上移动和向右移动的骑士(因此每一次移动都是x+=1, y+=2或x+=2, y+=1 ),您可以将a1+a2最小化,但前提是2*a1+a2 == x2-x1, a1+2*a2 == y2-y1, a1 >= 0, a2 >= 0。虽然ILPs通常是NP-完全的,但我希望一个标准爬山算法能够相当有效地解决它。
https://stackoverflow.com/questions/25233353
复制相似问题

