问为什么二进制堆必须是一个完整的二叉树？

EN

根据您提供的维基百科文章，二进制堆必须同时符合堆属性(正如您讨论过的那样)和形状属性(它要求它是一个完整的二叉树)。如果没有shape属性，就会失去数据结构提供的运行时优势(即完整性确保在删除元素时有一种定义良好的方法来确定新根，等等)。

数组中的每个项在二叉树中都有一个位置，这个位置是根据数组索引计算的。定位公式确保了树的“紧密包装”。

例如，这里的二叉树：

​

​

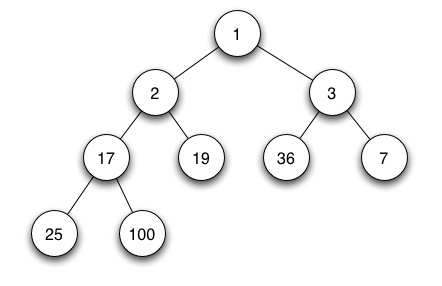
由数组表示。

[1, 2, 3, 17, 19, 36, 7, 25, 100].

注意，数组是按顺序排列的，就好像从树的顶部开始，然后从左到右读取每一行。

如果将另一项添加到此数组中，它将表示19下面的槽，以及100的右侧。如果这个新的数字小于19，那么值将不得不被交换，但无论如何，这是由数组的第10项填充的槽。

​

另一种看待它的方法是:尝试构建一个二进制堆，它不是一个完整的二叉树。你真的不能。

​

只有当树完成时，才能保证O(log(n))插入和(根)删除。原因如下：

如果树不完整，那么它可能是不平衡的，在最坏的情况下，它只是一个链表，要求O(n)查找叶子，O(n)用于插入和删除。有了完整性的形状要求，就可以保证O(log(n))操作，因为查找叶子(最后在数组中)需要一定的时间，并且保证树的深度不超过log2(N)，这意味着“冒泡向上”(用于插入)和“下沉”(用于删除)最多需要对堆中的数据进行log2(N)修改(交换)。

这就是说，您不一定要有一个完整的二叉树，但是您只是失去了这些运行时的保证。此外，正如其他人所提到的，拥有一个完整的二叉树可以轻松地将树存储为数组格式，而不是对象引用表示。