计算老虎机支出
一台老虎机有5个卷轴,每个卷轴显示3个符号(没有空格或“空”符号)。
支付可以通过多种方式进行。一些例子..。
- 出现一个特殊的钻石符号。
- 3幸运7出现
- 付款行中的所有五个符号都是相同的。
- 所有五个符号都是相同的数字,但颜色不同。
- 等。
此外,还需要检查多个支付行是否支付。
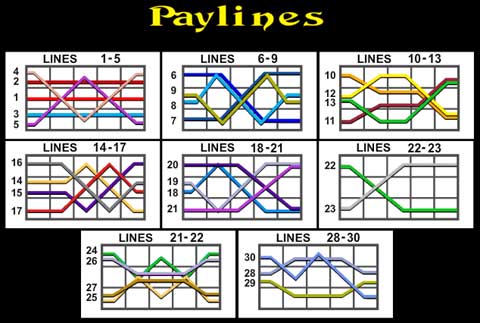
哪一种方法最能有效地计算每一圈的收益?或者,是否有比蛮力更有效的方法将每个支付方案应用于每个支付行?
回答 2
Stack Overflow用户
发布于 2014-08-18 23:46:01
除了支付宝外,每一笔支出都显得微不足道。对于三个幸运的7s,只需在可见的方块上迭代并计数7s。检查钻石也是一样的。如果我们让h是行数,w是列数,则这个操作是O(_h_w*),对于实际大小的老虎机来说,这个操作非常低。
不过,付费线路更有趣。理论上,支付宝的数量(从这里开始)要比*h ** w *大得多;在剔除跳过m= h^w的非法支付宝之前,它比*h ** w大得多。更重要的是,它们似乎有很多相似之处。例如,示例中的第2行和第6行都需要匹配左上角和左上角。如果这两条线不匹配,那么你就不能在第2行或第6行中获胜。
为了表示支付行,我将在范围1,h中使用长度w的整数数组,这样paylinei =解决方案中第一行的列(1索引)中的索引。例如,payline 1是1、1、1、1、1,而payline 17是3、3、2、1、2。
为此,后缀树似乎是一种适用的数据结构,它可以极大地提高您的运行时间,以便根据给定的板状态检查所有的付费行。请考虑下面的算法来构造封装所有付费行的后缀树。
Initialize:
Create a root node at column 0 (off-screen, non-column part of all solutions)
root node.length = 0
root node.terminal = false
Add all paylines (in the form of length w arrays of integers ranging from 1 to h) to the root nodes' "toDistribute set"
Create a toWork queue, add the root node to it
Iterate: while toWork not empty:
let node n = toWork.pop()
if n.length < w
create children of n with length n.length + 1 and terminal = (n.length + 1 == w).
for payline p in n.toDistribute
remove p from n.toDistribute
if(p.length > 1)
add p.subArray(1, end) to child of n as applicable.
add children of n to toWork在第1-11行的示例中运行此构造算法将给出如下所示的树:

这棵树的计算相当密集;它涉及创建sum i = 1 to w of h ^ i节点。树的大小仅取决于板的大小(高度和宽度),而不是支付行的数目,这是这种方法的主要优点。另一个好处是,这都是预处理;你可以在玩家坐下来拉杠杆之前建这棵树。
一旦建立了树,就可以为每个匹配条件(相同的符号、相同的颜色等)给每个节点一个字段。然后,在评估板状态时,您可以对树进行dfs,在每个新节点上,询问(对于每个标准)它是否与其父节点匹配。如果是,将该标准标记为true并继续。否则,将其标记为false,而不对孩子进行搜索以获得该标准。例如,如果您专门在子数组1、1上寻找相同的令牌,.如果发现第1列的第1行和第2列的第1行不匹配,那么包含1,1,.的任何付费行都不可能获胜,您也不必在树的这一部分中使用dfs。
要对这种dfs方法的效率进行彻底的算法分析,要比单独检查每个付费行要有效得多很难,因为这样的分析需要知道付费行之间的左侧重叠(平均)有多少。当然不会更糟,至少对你来说是个很好的例子。此外,添加到板中的付费行越多,重叠就越多,使用这种方法检查所有支付行的时间也就越省。
Stack Overflow用户
发布于 2016-03-17 18:34:34
为了计算RTP,您应该有完整的老虎机信息。最重要的部分是卷取条。蒙特卡罗通常是为了获得所需的统计数据而进行的。例如:https://raw.githubusercontent.com/VelbazhdSoftwareLLC/BugABoomSimulator/master/Main.cs
可付费信息:
private static int[][] paytable = {
new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0},
new int[]{0,0,0,0,0,0,0,0,0,0,0,0,0},
new int[]{0,0,0,0,0,0,0,0,2,2,2,10,2},
new int[]{5,5,5,10,10,10,15,15,25,25,50,250,5},
new int[]{25,25,25,50,50,50,75,75,125,125,250,2500,0},
new int[]{125,125,125,250,250,250,500,500,750,750,1250,10000,0},
};投注线:
private static int[][] lines = {
new int[]{1,1,1,1,1},
new int[]{0,0,0,0,0},
new int[]{2,2,2,2,2},
new int[]{0,1,2,1,0},
new int[]{2,1,0,1,2},
new int[]{0,0,1,2,2},
new int[]{2,2,1,0,0},
new int[]{1,0,1,2,1},
new int[]{1,2,1,0,1},
new int[]{1,0,0,1,0},
new int[]{1,2,2,1,2},
new int[]{0,1,0,0,1},
new int[]{2,1,2,2,1},
new int[]{0,2,0,2,0},
new int[]{2,0,2,0,2},
new int[]{1,0,2,0,1},
new int[]{1,2,0,2,1},
new int[]{0,1,1,1,0},
new int[]{2,1,1,1,2},
new int[]{0,2,2,2,0},
};卷轴条:
private static int[][] baseReels = {
new int[]{0,4,11,1,3,2,5,9,0,4,2,7,8,0,5,2,6,10,0,5,1,3,9,4,2,7,8,0,5,2,6,9,0,5,2,4,10,0,5,1,7,9,2,5},
new int[]{4,1,11,2,7,0,9,5,1,3,8,4,2,6,12,4,0,3,1,8,4,2,6,0,10,4,1,3,2,12,4,0,7,1,8,2,4,0,9,1,6,2,8,0},
new int[]{1,7,11,5,1,7,8,6,0,3,12,4,1,6,9,5,2,7,10,1,3,2,8,1,3,0,9,5,1,3,10,6,0,3,8,7,1,6,12,3,2,5,9,3},
new int[]{5,2,11,3,0,6,1,5,12,2,4,0,10,3,1,7,3,2,11,5,4,6,0,5,12,1,3,7,2,4,8,0,3,6,1,4,12,2,5,7,0,4,9,1},
new int[]{7,0,11,4,6,1,9,5,10,2,7,3,8,0,4,9,1,6,5,10,2,8,3},
};
private static int[][] freeReels = {
new int[]{2,4,11,0,3,7,1,4,8,2,5,6,0,5,9,1,3,7,2,4,10,0,3,1,8,4,2,5,6,0,4,1,10,5,2,3,7,0,5,9,1,3,6},
new int[]{4,2,11,0,5,2,12,1,7,0,9,2,3,0,12,2,4,0,5,8,2,6,0,12,2,7,1,3,10,6,0},
new int[]{1,4,11,2,7,8,1,5,12,0,3,9,1,7,8,1,5,12,2,6,10,1,4,9,3,1,8,0,12,6,9},
new int[]{6,4,11,2,7,3,9,1,6,5,12,0,4,10,2,3,8,1,7,5,12,0},
new int[]{3,4,11,0,6,5,3,8,1,7,4,9,2,5,10,0,3,8,1,4,10,2,5,9},
};为了计算RTP,应该多次调用自旋函数:
private static void spin(int[][] reels) {
for (int i = 0, r, u, d; i < view.Length && i < reels.Length; i++) {
if (bruteForce == true) {
u = reelsStops [i];
r = u + 1;
d = u + 2;
} else {
u = prng.Next (reels [i].Length);
r = u + 1;
d = u + 2;
}
r = r % reels[i].Length;
d = d % reels[i].Length;
view[i][0] = reels[i][u];
view[i][1] = reels[i][r];
view[i][2] = reels[i][d];
}
}每次旋转之后,所有的胜利都应该被计算出来。
https://stackoverflow.com/questions/25368309
复制相似问题

