gaussian_filter和gaussian_kde中西格玛与带宽的关系
如果适当地选择每个函数中的过滤器和bw_method参数,则在给定数据集上应用sigma和bw_method函数可以得到非常相似的结果。
例如,我可以通过在sigma=2.中设置gaussian_filter (左图)和在gaussian_kde中设置bw_method=sigma/30. (右图)来获得点的随机2D分布:
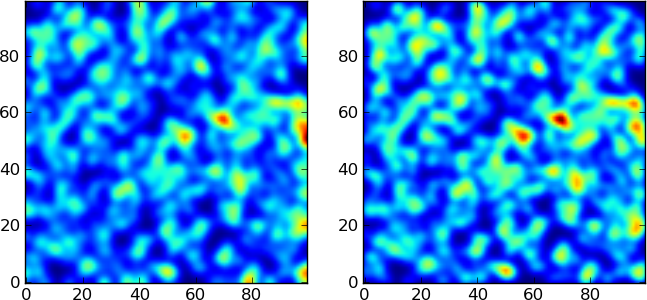
( MWE位于问题的底部)
显然,这些参数之间有关系,因为一个应用高斯滤波器,另一个对数据应用高斯核密度估计。
每个参数的定义是:
- 过滤器,
sigma
sigma :高斯核的标量或标量标准差序列。高斯滤波器的标准差是以一个序列或一个单数的形式给出的,在这种情况下,它对所有轴都是相等的。
考虑到高斯算子的定义,我可以理解这个问题:
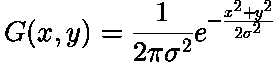
- kde,
bw_method
bw_method : str,标量或可调用,可选的方法用于计算估计器带宽。这可以是‘scott’,‘silverman’,一个标量常数或可调用的。如果是标量,这将直接用作kde.factor。如果是可调用的,它应该只接受一个gaussian_kde实例作为参数,并返回一个标量。如果没有(默认),则使用“scott”。有关更多细节,请参见备注。
在这种情况下,让我们假设bw_method的输入是标量(浮点),以便与sigma进行比较。这里是我迷路的地方,因为我在任何地方都找不到关于这个kde.factor参数的信息。
我想知道的是,如果可能的话,将这两个参数(即,使用浮点数时的sigma和bw_method )连接起来的精确的数学方程。
MWE:
import numpy as np
from scipy.stats import gaussian_kde
from scipy.ndimage.filters import gaussian_filter
import matplotlib.pyplot as plt
def rand_data():
return np.random.uniform(low=1., high=200., size=(1000,))
# Generate 2D data.
x_data, y_data = rand_data(), rand_data()
xmin, xmax = min(x_data), max(x_data)
ymin, ymax = min(y_data), max(y_data)
# Define grid density.
gd = 100
# Define bandwidth
bw = 2.
# Using gaussian_filter
# Obtain 2D histogram.
rang = [[xmin, xmax], [ymin, ymax]]
binsxy = [gd, gd]
hist1, xedges, yedges = np.histogram2d(x_data, y_data, range=rang, bins=binsxy)
# Gaussian filtered histogram.
h_g = gaussian_filter(hist1, bw)
# Using gaussian_kde
values = np.vstack([x_data, y_data])
# Data 2D kernel density estimate.
kernel = gaussian_kde(values, bw_method=bw / 30.)
# Define x,y grid.
gd_c = complex(0, gd)
x, y = np.mgrid[xmin:xmax:gd_c, ymin:ymax:gd_c]
positions = np.vstack([x.ravel(), y.ravel()])
# Evaluate KDE.
z = kernel(positions)
# Re-shape for plotting
z = z.reshape(gd, gd)
# Make plots.
fig, (ax1, ax2) = plt.subplots(1, 2)
# Gaussian filtered 2D histograms.
ax1.imshow(h_g.transpose(), origin='lower')
ax2.imshow(z.transpose(), origin='lower')
plt.show()回答 1
Stack Overflow用户
发布于 2014-09-24 08:51:27
没有关系,因为你在做两件不同的事情。
使用scipy.ndimage.filters.gaussian_filter,您将使用内核过滤2D变量(图像),而该内核恰好是高斯的。它实质上是平滑图像。
使用scipy.stats.gaussian_kde,您尝试估计2D变量的概率密度函数。带宽(或平滑参数)是您的集成步骤,应该在数据允许的范围内尽可能小。
这两幅图像看起来是一样的,因为你画样本的均匀分布和正态分布并没有多大区别。很明显,用一个正常的核函数可以得到一个更好的估计。
你可以读到关于核密度估计的文章。
编辑:在核密度估计(KDE)中,核的尺度使得带宽是平滑核的标准偏差。使用哪种带宽并不明显,因为它取决于数据。单变量数据存在一个最佳选择,称为Silverman的经验法则。
总之,高斯滤波器的标准差和KDE的带宽之间没有关系,因为我们谈论的是橘子和苹果。然而,说到KDE 仅限于,KDE带宽与同一KDE内核的标准差之间存在着某种关系。他们是平等的!实际上,实现细节是不同的,并且可能会根据内核的大小进行缩放。您可以阅读您的特定包gaussian_kde.py
https://stackoverflow.com/questions/25750774
复制相似问题

