文档建议反馈控制台
首页
学习
活动
专区
圈层
工具
MCP广场
文章/答案/技术大牛
发布
首页
学习
活动
专区
圈层
工具
MCP广场
返回腾讯云官网
社区首页 >问答首页 >瓦特裂变谱上的Sage积分失败

问瓦特裂变谱上的Sage积分失败
EN

Stack Overflow用户
提问于 2014-09-18 05:44:27
回答 2查看 128关注 0票数 1

我试图用Sage来整合瓦特裂变光谱(命令在下面)，但是当我这样做的时候，我注意到积分的结果是没有意义的。瓦特裂变光谱是一个pdf，当集成从0到10应该是大约一个(由沃尔夫拉姆阿尔法确认)。对于Sage，当下限接近于0时，积分为负值，当下限接近1时，积分为正。

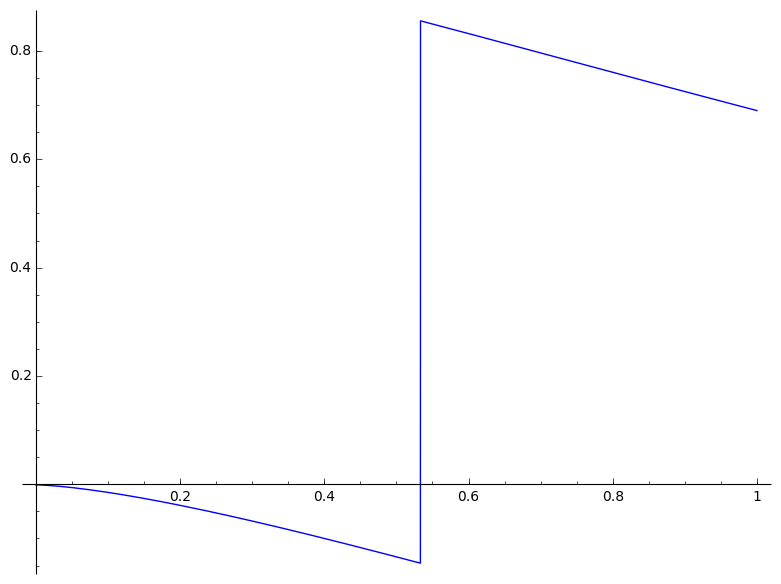
下面是瓦特裂变谱与x to 10与x与0 to 1的边界积分的一幅图。跳得很清楚。

我如何纠正这一点，并有信心在未来的积分是正确的评估？

代码语言：javascript
运行
复制
var('o')
assume(x>10)
plot(integral(0.453*exp(-1.036*o)*sinh(sqrt(2.29*o)), (o, x, 10)), (x,0,1))

​

​

根据Robert的建议，我尝试了以下整合：

代码语言：javascript
运行
复制
map(var, 'abcde')
assume(e-d>0)
foo(a,b,c,d,e) = integral(a*exp(b*o)*sinh(sqrt(c*o)), (o, d, e))
float(foo(*map(QQ, [0.453,-1.036,2.29,0,10])))

这仍然返回-0.0010615612261540579的值。

numerical-integration
python
sympy
symbolic-math
sage
EN

回答 2

Stack Overflow用户

回答已采纳

发布于 2014-09-18 19:08:07

我不知道为什么Sage不传递Maxima的问题，但是如果没有这些问题，您就不能(在Sage中)判断结果因参数不同而不同。

这是极大值的一个推导。我将积分从0改为x，而不是x为10，因为积分器是pdf，所以随着x的增加，积分从0变为1。

原始公式。

代码语言：javascript
运行
复制
(%i2) foo : 0.453*exp(-1.036*o)*sinh(sqrt(2.29*o)) $

用符号而不是数字来表达。

代码语言：javascript
运行
复制
(%i3) foo1 : a * exp(-b*o) * sinh(sqrt(c*o)) $

提前回答integrate的一些问题。这样做并不是绝对必要的；如果不给出这些假设，integrate只会提出额外的问题。

代码语言：javascript
运行
复制
(%i4) assume (equal (a, ratsimp (0.453)), equal (b, ratsimp (1.036)), equal (c, ratsimp (2.29))) $

rat: replaced 0.453 by 453/1000 = 0.453

rat: replaced 1.036 by 259/250 = 1.036

rat: replaced 2.29 by 229/100 = 2.29
(%i5) assume (x > 0) $

计算积分。integrate询问与参数a、b和c有关的x。我会依次给出每个答案，看看我得到了什么。I1、I2和I3是所有答案的结果。我将首先回答p (阳性)。

代码语言：javascript
运行
复制
(%i6) I1 : integrate (foo1, o, 0, x);
Is 4*b^2*x-c positive, negative or zero?

p;
(%o6) a*(-gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
        *sqrt(c)*%e^(c/(4*b))*sqrt(x)
        /(2*sqrt(b)*abs(2*b*sqrt(x)-sqrt(c)))
        +gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *c*%e^(c/(4*b))
         /(4*b^(3/2)*abs(2*b*sqrt(x)-sqrt(c)))
        -gamma_incomplete(1/2,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *sqrt(c)*%e^(c/(4*b))
         /(4*b^(3/2))+sqrt(%pi)*sqrt(c)*%e^(c/(4*b))/(2*b^(3/2))
        +gamma_incomplete(1,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *%e^(c/(4*b))
         /(2*b)
        -gamma_incomplete(1,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *%e^(c/(4*b))
         /(2*b))

现在我将回答n (否定)。

代码语言：javascript
运行
复制
(%i7) I2 : integrate (foo1, o, 0, x);
Is 4*b^2*x-c positive, negative or zero?

n;
(%o7) a*(-gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
        *sqrt(c)*%e^(c/(4*b))*sqrt(x)
        /(2*sqrt(b)*abs(2*b*sqrt(x)-sqrt(c)))
        +gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *c*%e^(c/(4*b))
         /(4*b^(3/2)*abs(2*b*sqrt(x)-sqrt(c)))
        -gamma_incomplete(1/2,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *sqrt(c)*%e^(c/(4*b))
         /(4*b^(3/2))
        +gamma_incomplete(1,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *%e^(c/(4*b))
         /(2*b)
        -gamma_incomplete(1,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *%e^(c/(4*b))
         /(2*b))

现在是z (0)。

代码语言：javascript
运行
复制
(%i8) I3 : integrate (foo1, o, 0, x);
Is 4*b^2*x-c positive, negative or zero?

z;
(%o8) a*(-gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
        *sqrt(c)*%e^(c/(4*b))*sqrt(x)
        /(2*sqrt(b)*abs(2*b*sqrt(x)-sqrt(c)))
        +gamma_incomplete(1/2,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *c*%e^(c/(4*b))
         /(4*b^(3/2)*abs(2*b*sqrt(x)-sqrt(c)))
        -gamma_incomplete(1/2,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *sqrt(c)*%e^(c/(4*b))
         /(4*b^(3/2))
        +gamma_incomplete(1,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
         *%e^(c/(4*b))
         /(2*b)
        -gamma_incomplete(1,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
         *%e^(c/(4*b))
         /(2*b))

我看不出其中的一些结果是否是相同的。让我们来检查一下。

代码语言：javascript
运行
复制
(%i9) is (I1 = I2);
(%o9) false
(%i10) is (I1 = I3);
(%o10) false
(%i11) is (I2 = I3);
(%o11) true

好的，有两个不同的结果：I1 (应答p)和I2 (应答n和z)。我将把这两个问题放在一个条件表达式中，其中测试是integrate提出的问题。请注意，c/(4*b^2)大约是0.533，这似乎是OP显示的图的跳跃点。

代码语言：javascript
运行
复制
(%i12) I : if x < c/(4*b^2) then ''I2 else ''I1;
(%o12) if x < c/(4*b^2)
           then a*(-gamma_incomplete(1/2,
                                     -(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                  *sqrt(c)*%e^(c/(4*b))*sqrt(x)
                  /(2*sqrt(b)*abs(2*b*sqrt(x)-sqrt(c)))
                  +gamma_incomplete(1/2,
                                    -(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                   *c*%e^(c/(4*b))
                   /(4*b^(3/2)*abs(2*b*sqrt(x)-sqrt(c)))
                  -gamma_incomplete(1/2,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
                   *sqrt(c)*%e^(c/(4*b))
                   /(4*b^(3/2))
                  +gamma_incomplete(1,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
                   *%e^(c/(4*b))
                   /(2*b)
                  -gamma_incomplete(1,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                   *%e^(c/(4*b))
                   /(2*b))
           else a*(-gamma_incomplete(1/2,
                                     -(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                  *sqrt(c)*%e^(c/(4*b))*sqrt(x)
                  /(2*sqrt(b)*abs(2*b*sqrt(x)-sqrt(c)))
                  +gamma_incomplete(1/2,
                                    -(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                   *c*%e^(c/(4*b))
                   /(4*b^(3/2)*abs(2*b*sqrt(x)-sqrt(c)))
                  -gamma_incomplete(1/2,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
                   *sqrt(c)*%e^(c/(4*b))
                   /(4*b^(3/2))+sqrt(%pi)*sqrt(c)*%e^(c/(4*b))/(2*b^(3/2))
                  +gamma_incomplete(1,(4*b^2*x+4*b*sqrt(c)*sqrt(x)+c)/(4*b))
                   *%e^(c/(4*b))
                   /(2*b)
                  -gamma_incomplete(1,-(-4*b^2*x+4*b*sqrt(c)*sqrt(x)-c)/(4*b))
                   *%e^(c/(4*b))
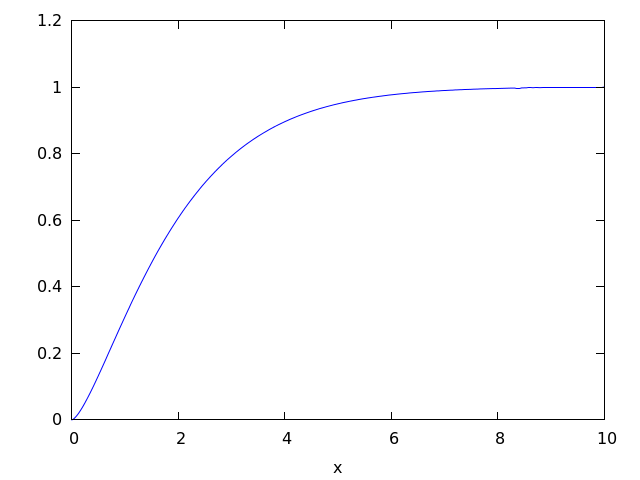
                   /(2*b))

现在我来画这个。plot2d由临时绑定到特定值的a、b和c计算。情节看上去和预期的一样。

代码语言：javascript
运行
复制
(%i13) plot2d (I, [x, 0, 10]), a=0.453, b=1.036, c=2.29;

​

​

票数 0
EN

Stack Overflow用户

发布于 2014-09-18 16:37:50

在默认情况下，Sage会以极大值( Maxima )来计算积分。Maxima本身提出了一些关于几个变量的符号的问题，并给出了对这些问题的不同答案，得到不同的结果。我想这些问题在Sage/Maxima界面中被弄丢了。Sage也可以调用Sympy来计算积分，但是我发现Sympy不能解决这个积分。

请记住，Maxima对确切的数字(即积分和理据)比不精确(即浮动)更舒服。我的建议是用理性或符号代替浮标(后来用数值代替符号)。

考虑到不同的结果，您可以拼凑一个类似于if <condition 1> then <result 1> else if <condition 2> then <result 2> else ...的函数。目前还没有任何好的方法来自动做到这一点。(我开发了一个名为noninteractive的实验包，但我不能推荐它用于一般用途；自己构建if--then更可靠。)

这里是一个Maxima会话，显示了第一个案例。你可以通过给出不同的答案(正、负、零)来得到其他的答案。我还没有检查结果，但第一步是整理不同的案例。

代码语言：javascript
运行
复制
(%i2) foo : 0.453*exp(-1.036*o)*sinh(sqrt(2.29*o)) $
(%i3) bar : ratsimp (foo);

rat: replaced -1.036 by -259/250 = -1.036

rat: replaced 1.513274595042156 by 35244471/23290202 = 1.513274595042156

rat: replaced 0.453 by 453/1000 = 0.453
(%o3) 453*sinh(35244471*sqrt(o)/23290202)*%e^-(259*o/250)/1000
(%i4) I1 : integrate (bar, o, x, 10);
Is 36386982230699133124*x-19408949001091265625 positive, negative or zero?

p;
Is x-344460873305900065615/36386982230699133124 positive, negative or zero?

p;
(%o4) 453*(22027794375*sqrt(10)*%e^(155271592008730125/280980557766016472)
                      *gamma_incomplete(1/2,
                                        -(-36386982230699133124*x
                                         +53150092471010944500*sqrt(x)
                                         -19408949001091265625)
                                         /35122569720752059000)*sqrt(x)
          /(2*sqrt(259)*abs(6032162318*sqrt(x)-4405558875))
          -97044745005456328125*sqrt(10)
                               *%e^(155271592008730125/280980557766016472)
                               *gamma_incomplete(1/2,
                                                 -(-36386982230699133124*x
                                                  +53150092471010944500
                                                   *sqrt(x)
                                                  -19408949001091265625)
                                                  /35122569720752059000)
           /(46580404*259^(3/2)*abs(6032162318*sqrt(x)-4405558875))
          -125*%e^(155271592008730125/280980557766016472)
              *gamma_incomplete(1,
                                (36386982230699133124*x
                                 +53150092471010944500*sqrt(x)
                                 +19408949001091265625)
                                 /35122569720752059000)
           /259
          +125*%e^(155271592008730125/280980557766016472)
              *gamma_incomplete(1,
                                -(-36386982230699133124*x
                                 +53150092471010944500*sqrt(x)
                                 -19408949001091265625)
                                 /35122569720752059000)
           /259
          +291127525*10^(3/2)*%e^(155271592008730125/280980557766016472)
                    *gamma_incomplete(1,
                                      (106300184942021889*10^(5/2)
                                       +76655754261616519373)
                                       /7024513944150411800)
           /(6032162318*sqrt(10)-4405558875)
          -550694859375*%e^(155271592008730125/280980557766016472)
                       *gamma_incomplete(1,
                                         (106300184942021889*10^(5/2)
                                          +76655754261616519373)
                                          /7024513944150411800)
           /(259*(6032162318*sqrt(10)-4405558875))
          -291127525*10^(3/2)*%e^(155271592008730125/280980557766016472)
                    *gamma_incomplete(1,
                                      -(106300184942021889*10^(5/2)
                                       -76655754261616519373)
                                       /7024513944150411800)
           /(6032162318*sqrt(10)-4405558875)
          +550694859375*%e^(155271592008730125/280980557766016472)
                       *gamma_incomplete(1,
                                         -(106300184942021889*10^(5/2)
                                          -76655754261616519373)
                                          /7024513944150411800)
           /(259*(6032162318*sqrt(10)-4405558875))
          +22027794375*sqrt(10)*%e^(155271592008730125/280980557766016472)
                      *gamma_incomplete(1/2,
                                        (36386982230699133124*x
                                         +53150092471010944500*sqrt(x)
                                         +19408949001091265625)
                                         /35122569720752059000)
           /(46580404*259^(3/2))
          -110138971875*%e^(155271592008730125/280980557766016472)
                       *gamma_incomplete(1/2,
                                         (106300184942021889*10^(5/2)
                                          +76655754261616519373)
                                          /7024513944150411800)
           /((6032162318*sqrt(10)-4405558875)*sqrt(259))
          +97044745005456328125*sqrt(10)
                               *%e^(155271592008730125/280980557766016472)
                               *gamma_incomplete(1/2,
                                                 (106300184942021889*10^(5/2)
                                                  +76655754261616519373)
                                                  /7024513944150411800)
           /(46580404*(6032162318*sqrt(10)-4405558875)*259^(3/2))
          -110138971875*%e^(155271592008730125/280980557766016472)
                       *gamma_incomplete(1/2,
                                         -(106300184942021889*10^(5/2)
                                          -76655754261616519373)
                                          /7024513944150411800)
           /((6032162318*sqrt(10)-4405558875)*sqrt(259))
          +97044745005456328125*sqrt(10)
                               *%e^(155271592008730125/280980557766016472)
                               *gamma_incomplete(1/2,
                                                 -(106300184942021889*10^(5/2)
                                                  -76655754261616519373)
                                                  /7024513944150411800)
           /(46580404*(6032162318*sqrt(10)-4405558875)*259^(3/2)))
 /1000
票数 0
EN
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接：

https://stackoverflow.com/questions/25905006

复制
相关文章

相似问题

领券

腾讯云开发者

扫码关注腾讯云开发者

扫码关注腾讯云开发者

领取腾讯云代金券

热门产品

热门推荐

更多推荐

Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有 

深圳市腾讯计算机系统有限公司 ICP备案/许可证号：粤B2-20090059 深公网安备号 44030502008569

腾讯云计算（北京）有限责任公司 京ICP证150476号 |  京ICP备11018762号 | 京公网安备号11010802020287

问题归档专栏文章快讯文章归档关键词归档开发者手册归档开发者手册 Section 归档