问在GLSL上的鲁棒atan(y，x)将XY坐标转换成角度

EN

我要回答我自己的问题来分享我的知识。我们首先注意到，当x接近于零时，不稳定性就会发生。但是，我们也可以将其翻译为abs(x) << abs(y)。首先，我们将平面(假设我们位于一个单位圆上)划分为两个区域:一个是|x| <= |y|区域，另一个是|x| > |y|区域，如下所示：

​

​

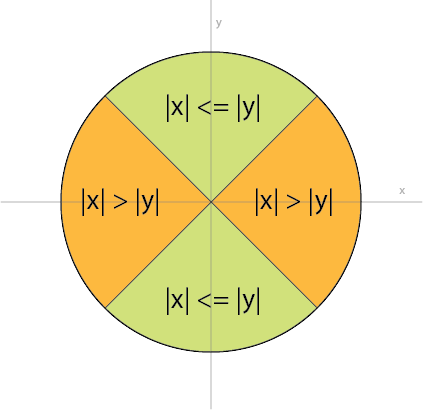
我们知道，atan(x,y)在绿色区域要稳定得多--当x接近于零时，我们只是有接近atan(0.0)的东西，这在数值上是非常稳定的，而通常的atan(y,x)在橙色区域则更稳定。你也可以说服自己，这种关系：

atan(x,y) = PI/2 - atan(y,x)

对于所有未定义的非原点(x，y)，我们讨论的是atan(y,x)，它能够在整个-PI、PI、而不是只返回-PI/2、PI/2之间的角度的范围内返回角值。因此，我们针对GLSL的健壮atan2()例程非常简单：

float atan2(in float y, in float x)
{
    bool s = (abs(x) > abs(y));
    return mix(PI/2.0 - atan(x,y), atan(y,x), s);
}

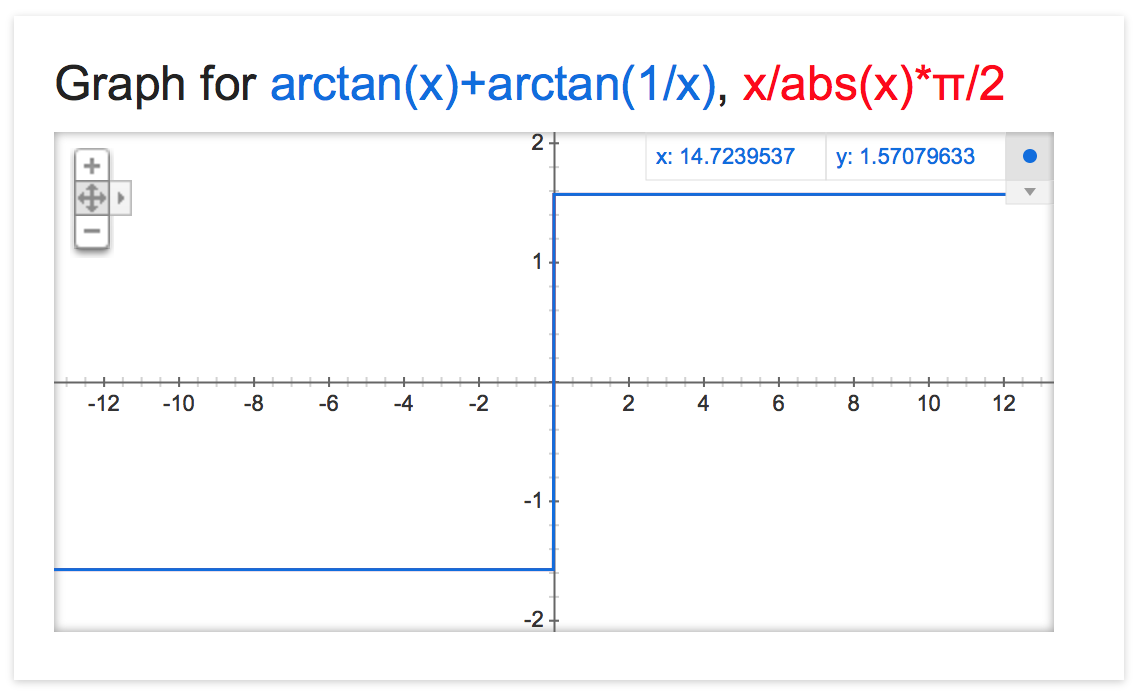
顺便提一下，数学函数atan(x)的恒等式实际上是：

atan(x) + atan(1/x) = sgn(x) * PI/2

这是正确的，因为它的范围是(-PI/2，PI/2)。

​

​

取决于您的目标平台，这可能是一个解决问题。atan(y, x)指定它应该在所有象限中工作，只有当x和y都是0时，才会有未定义的行为。

因此，会期望任何良好的实现都能在所有轴附近稳定，因为这就是2参数atan (或atan2)背后的全部目的。

发问者/应答者是正确的，因为有些实现确实采用快捷方式。但是，接受的解决方案假设，当x接近于零时，坏的实现总是不稳定的:在某些硬件(例如我的Galaxy S4 )中，当 x 接近于零时，值是稳定的，而当 y 接近于0E 216时，则不稳定。

为了测试GLSL呈现器的atan(y,x)实现，下面是一个WebGL测试模式。按照下面的链接，只要您的OpenGL实现是体面的，您就会看到如下所示：

​

​

使用本机atan(y,x)**:** http://glslsandbox.com/e#26563.2的测试模式

如果一切顺利，您应该看到8种不同的颜色(忽略中心)。

链接的示例为x和y的几个值(包括0、非常大和非常小的值)提供了atan(y,x)示例。中心框是atan(0.,0.)--数学上没有定义，实现也各不相同。我在我测试过的硬件上看到了0(红色)、PI/2 (绿色)和NaN (黑色)。

下面是可接受的解决方案的测试页面。注意:主机的WebGL版本缺少mix(float,float,bool)，所以我添加了一个与规范相匹配的实现。

使用atan2(y,x) 的测试模式(来自公认答案： http://glslsandbox.com/e#26666.0 )

在x=y=0的情况下，建议的解决方案仍然失败。这里，两个atan()函数都返回NaN。

此外，我也不希望在这两种情况下进行混合。我不确定这是如何实现/编译的，但是IEEE浮动规则x*NaN和x+NaN的结果在NaN中再次出现。因此，如果您的编译器确实使用了mix/插值，那么结果应该是NaN，用于x=0或y=0。

下面是另一个解决问题的方法：

float atan2(in float y, in float x)
{
    return x == 0.0 ? sign(y)*PI/2 : atan(y, x);
}

当x=0时，角度可以是±π/2，两者中的哪一个只依赖于y。如果y=0也是，角度可以是任意的(向量的长度为0)。在这种情况下，sign(y)返回0，这很好。