有限滤波器快速一维卷积与python中dirac三角和
有限滤波器快速一维卷积与python中dirac三角和
提问于 2014-09-30 13:11:48
我需要计算以下卷积:
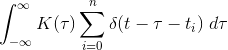
K是一个非常简单的滤波器,它只是一个有限的矩形盒(!)大小。我的数据是狄拉克三角洲时代t_i的列表。
直截了当的解决办法是将数据存放起来,并使用numpy或bin的卷积函数之一。但是,还有更快的方法吗?我是否可以避免数据的绑定,并利用这样的事实:( a)我的过滤器的大小是有限的(只是一个框)和( b)我有一个时间点列表。因此,我只需要检查我的时间点目前是否是滑动框的一部分。
因此,我正在寻找一个复杂度为O(d*n)的解,其大小与卷积的分辨率相同。因此,我想要比O(b**2)要快得多,因为有b的桶数。此外,由于n << b,它仍然认为,对于基于fft的卷积,O(d*n)远小于O(b * log b)。谢谢!
回答 1
Stack Overflow用户
回答已采纳
发布于 2014-09-30 13:21:17
使用信号累积和可以加速带大盒滤波器的卷积
示例信号:
import numpy as np
a = np.random.rand(10)
print a输出:
[ 0.22501645 0.46078123 0.6788864 0.88293584 0.10379173 0.50422604
0.4670648 0.22018486 0.96649785 0.44451671]利用缺省卷积函数实现卷积
print np.convolve(a, np.ones(3) / 3, mode='valid')输出:
[ 0.45489469 0.67420116 0.55520466 0.49698454 0.35836086 0.39715857
0.55124917 0.54373314]使用累积和的卷积:
s = np.cumsum(np.concatenate(([0], a)))
print (s[3:] - s[:-3]) / 3输出:
[ 0.45489469 0.67420116 0.55520466 0.49698454 0.35836086 0.39715857
0.55124917 0.54373314]cumsum计算和列表减法都是O(n),n是列表元素的数目,因此计算的总时间是O(n),而且-有趣的是,与滤波器大小无关。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/26121770
复制相关文章
相似问题

