是什么使一项任务很难或“复杂”的机器学习?关于模式的复杂性,而不是在计算上
是什么使一项任务很难或“复杂”的机器学习?关于模式的复杂性,而不是在计算上
提问于 2014-12-07 06:18:08
和很多人一样,我对机器学习感兴趣。我已经上了一堂关于这个话题的课,并且一直在读一些论文。我有兴趣找出是什么使机器学习很难解决问题。理想情况下,我想了解如何量化或表达机器学习问题的复杂性。
显然,如果一个模式有很大的噪声,人们可以查看不同算法的更新技术,并观察到某些特定的机器学习算法由于有噪声的标签而不正确地将自己更新到错误的方向,但这是非常定性的争论,而不是某种分析/量化的推理。
那么,如何量化问题或模式的复杂性来反映机器学习算法所面临的困难呢?也许是信息论之类的东西,我真的没有什么想法。
回答 1
Stack Overflow用户
回答已采纳
发布于 2014-12-07 07:43:35
在机器学习中,域的VC维数通常用来分类“学习它有多难”。
如果存在一组k样本,则该域据说具有k的VC维度,因此无论它们的标签是什么,建议的模型都可以“粉碎它们”(使用模型的某些配置将它们完美地分割开来)。
wikipedia页面提供了2D示例作为域,并以线性分隔器作为模型:
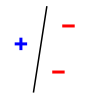
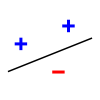
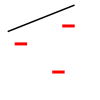
以上试图证明在2D中有一个点的设置,这样一个人可以安装一个线性分离器来分割它们,不管标签是什么。然而,对于2D中的每4个点,都有一些标签的赋值,因此线性分隔器不能将它们分开:
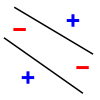
因此,具有线性分离器的二维空间的VC维数为3。
此外,如果一个领域和模型的VC维数是无穷大的,则说这个问题是不可学习的。
如果你有足够强的数学背景,并且对机器学习理论感兴趣,你可以尝试遵循Amnon Shashua关于PAC的讲座。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/27340208
复制相关文章
相似问题

