微调stat_ellipse()在ggplot2中
微调stat_ellipse()在ggplot2中
提问于 2014-12-09 15:07:05
我想用95%的“精确”置信椭圆建立二元正态分布的散点图。
library(mvtnorm)
library(ggplot2)
set.seed(1)
n <- 1e3
c95 <- qchisq(.95, df=2)
rho <- 0.8 #correlation
Sigma <- matrix(c(1, rho, rho, 1), 2, 2) # Covariance matrix我用平均值为零和方差=Sigma的二元正常值生成了1000个观测值。
x <- rmvnorm(n, mean=c(0, 0), Sigma)
z <- p95 <- rep(NA, n)
for(i in 1:n){
z[i] <- x[i, ] %*% solve(Sigma, x[i, ])
p95[i] <- (z[i] < c95)
}利用stat_ellipse可以方便地在生成的数据散点图顶部绘制95%的置信椭圆。最终的数字是完全令人满意的,直到你注意到几个红色点位于置信椭圆内。我想,这种差异来自于一些参数的估计,并且随着样本数量的增加而消失。
data <- data.frame(x, z, p95)
p <- ggplot(data, aes(X1, X2)) + geom_point(aes(colour = p95))
p + stat_ellipse(type = "norm")
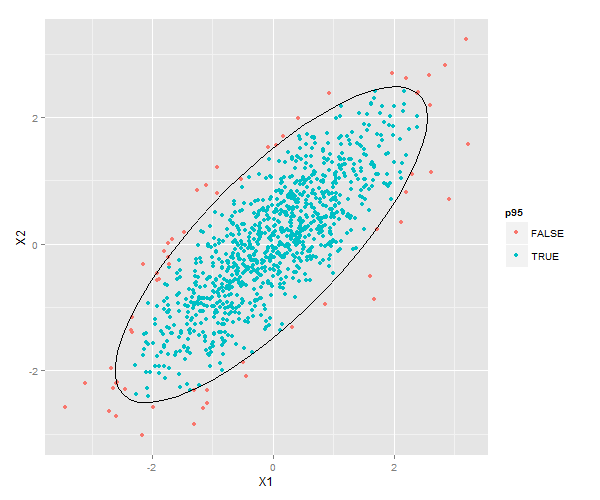
有没有任何方法来微调stat_ellipse(),使其描绘“精确”的置信椭圆,如下图所示,它是使用“手工”ellips函数创建的?
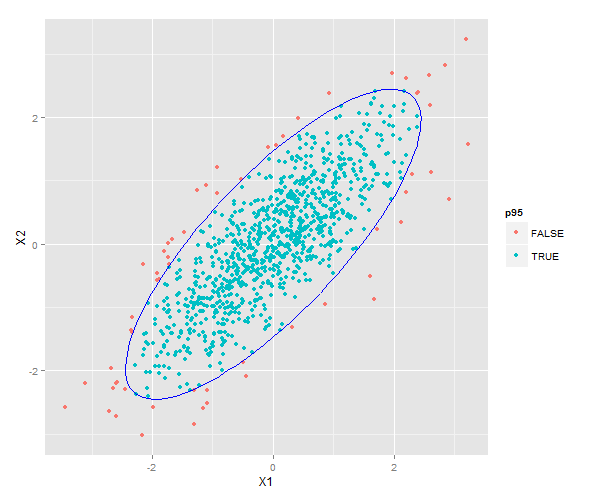
ellips <- function(center = c(0,0), c=c95, rho=-0.8, npoints = 100){
t <- seq(0, 2*pi, len=npoints)
Sigma <- matrix(c(1, rho, rho, 1), 2, 2)
a <- sqrt(c*eigen(Sigma)$values[2])
b <- sqrt(c*eigen(Sigma)$values[1])
x <- center[1] + a*cos(t)
y <- center[2] + b*sin(t)
X <- cbind(x, y)
R <- eigen(Sigma)$vectors
data.frame(X%*%R)
}
dat <- ellips(center=c(0, 0), c=c95, rho, npoints=100)
p + geom_path(data=dat, aes(x=X1, y=X2), colour='blue')回答 2
Stack Overflow用户
回答已采纳
发布于 2014-12-10 01:10:55
这不是一个真正的答案,但可能会有所帮助。
通过使用以下命令探索stat_ellipse,
stat_ellipse
ls(ggplot2:::StatEllipse)
ggplot2:::StatEllipse$calculate
ggplot2:::calculate_ellipse
?cov.wtcov.wt似乎正在从模拟数据中估计协方差矩阵:
cov.wt(data[, c(1, 2)])$cov
# X1 X2
# X1 1.1120267 0.8593946
# X2 0.8593946 1.0372208
# True covariance matrix:
Sigma
# [,1] [,2]
# [1,] 1.0 0.8
# [2,] 0.8 1.0您可以考虑使用估计的协方差矩阵计算p95值。或者坚持你自己执行良好的椭圆绘图代码。
Stack Overflow用户
发布于 2020-12-10 07:31:45
原问题中提出的椭圆码是错误的。当X1和X2变量的平均值为0,标准差为1时,它是有效的,但在一般情况下不起作用。
这里有一个替代的实现,它是从椭圆源代码中改编的。它以均值的向量、协方差矩阵、半径(例如用置信度计算)和形状的分段数作为参数。
calculate_ellipse <- function(center, shape, radius, segments){
# Adapted from https://github.com/tidyverse/ggplot2/blob/master/R/stat-ellipse.R
chol_decomp <- chol(shape)
angles <- (0:segments) * 2 * pi/segments
unit.circle <- cbind(cos(angles), sin(angles))
ellipse <- t(center + radius * t(unit.circle %*% chol_decomp))
colnames(ellipse) <- c("X1","X2")
as.data.frame(ellipse)
}让我们比较这两种实现:
library(ggplot2)
library(MASS) # mvrnorm function, to sample multivariate normal variables
set.seed(42)
mu = c(10, 20) # vector of means
rho = -0.7 # correlation coefficient
correlation = matrix(c(1, rho, rho, 1), 2) # correlation matrix
std = c(1, 10) # vector of standard deviations
sigma = diag(std) %*% correlation %*% diag(std) # covariance matrix
N = 1000 # number of points
confidence = 0.95 # confidence level for the ellipse
df = data.frame(mvrnorm(n=N, mu=mu, Sigma=sigma))
radius = sqrt(2 * stats::qf(confidence, 2, Inf)) # radius of the ellipse
ellips <- function(center = c(0,0), c=c95, rho=-0.8, npoints = 100){
# Original proposal
t <- seq(0, 2*pi, len=npoints)
Sigma <- matrix(c(1, rho, rho, 1), 2, 2)
a <- sqrt(c*eigen(Sigma)$values[2])
b <- sqrt(c*eigen(Sigma)$values[1])
x <- center[1] + a*cos(t)
y <- center[2] + b*sin(t)
X <- cbind(x, y)
R <- eigen(Sigma)$vectors
data.frame(X%*%R)
}
calculate_ellipse <- function(center, shape, radius, segments){
# Adapted from https://github.com/tidyverse/ggplot2/blob/master/R/stat-ellipse.R
chol_decomp <- chol(shape)
angles <- (0:segments) * 2 * pi/segments
unit.circle <- cbind(cos(angles), sin(angles))
ellipse <- t(center + radius * t(unit.circle %*% chol_decomp))
colnames(ellipse) <- c("X1","X2")
as.data.frame(ellipse)
}
ggplot(df) +
aes(x=X1, y=X2) +
theme_bw() +
geom_point() +
geom_path(aes(color="new implementation"), data=calculate_ellipse(mu, sigma, radius, 100)) +
geom_path(aes(color="original implementation"), data=ellips(mu, confidence, rho, 100))
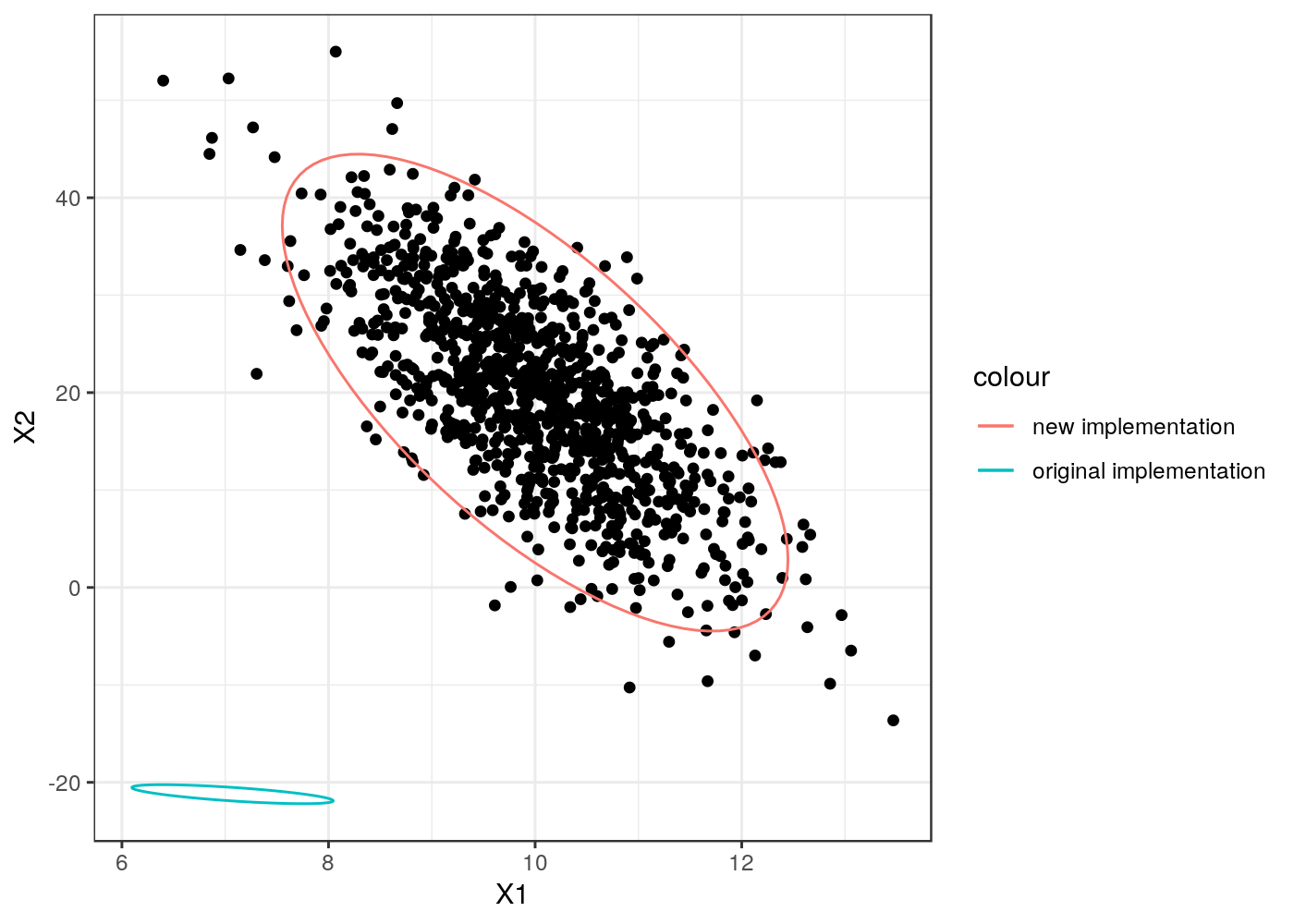
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/27382145
复制相关文章
相似问题

