寻找跨越给定最小生成树的最小权完全图
设T= (V,E)是一棵具有已知代价的|V|顶点和|E| = |V-1|边树。构造了一个最小权完全图G= (V,E'),它的最小生成树为T。
示例:假设下面的树T. red中的边有给定的成本。虚线边将被添加,以从这棵树构建一个完整的图。
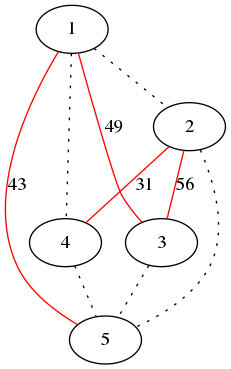
跨T作为其唯一MST的最小权重完整图G如下:
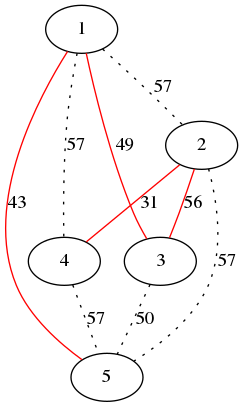
我试图找到一个生成这个图的(多项式时间)算法。我主要是找一个提示,而不是完整的解决方案。到目前为止,我已经设计了以下算法:
1)找出图中包含权重w_max的最大MST边和不包含其他MST边的割集。所有其他边缘都必须是w_max + 1。以下图片说明了我的想法:
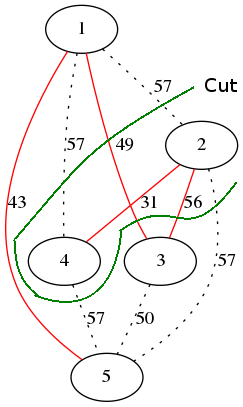
边(1-2),(1-4),(4-5),(2-3)和(2-5)被包含在这个切割C中。唯一包含在MST中的边缘是边缘(2-3),它是MST中最重的边缘,具有w=56。因此,所有其他边都应该有w=57。证明:假设相反;我们可以用另一条边替换(2-3),并保持树的连接。现在树的重量更轻了,因此(2-3)不属于MST。矛盾。
( 2)对所有其它边缘e_i,w_i,按重量顺序重复。取一个只包含e_i和其他MST边缘的剪切。任何未知的非MST边缘的这一削减,应该有一个重量的w_i + 1.
问题:
1)上述算法正确吗?根据裁剪的属性,应该是。
2)我能更有效地做这件事吗?我没有算法可以在我的头顶上找到划痕,但我不认为这种方法是有效的。
编辑:我脑海中的另一种方法是一种基于Kruskal算法的方法:
1)利用unify迭代所有MST边,提高代价,并将对应的顶点统一在同一分量下。
2)在每一步中,通过成本w的边缘将两个不同的组件统一起来。在同一(新)组件中形成循环的任何其他边缘都应该具有w+1的成本。
回答 1
Stack Overflow用户
发布于 2015-01-08 06:40:37
回答我自己的问题
下面是我想出的一个有效答案,也是来自@sasha的反馈。假设我们要计算完全图G的总权重,即;
设T= (V,E)是一棵具有已知权值的奇点树。计算最小权完全图G= (V,E')的总权
w_total,该图的最小生成树为T。注:边权值是自然数。
算法:
- 用
|V|单例组件初始化Union-Find。 - 按上升权重对
T的所有边缘进行排序。运行时间:O(log*log\V_x)。 - 迭代下一个边缘
e = (v1,v2)ofT。将其权重w_e添加到w_total。 - 在联盟中找到
v1和v2的组件--查找:set1,set2,分别包含size1和size2顶点。 - 这些组成部分将是统一的。由于
G是一个完整的图,所以将添加size1 × size2边:一个边是MSTe边,所有其他的边都要比e重,这样Kruskal的算法就会忽略它们。因此,它们的最小重量至少应该是w_e + 1。 w_total += (size1 × size2 - 1) × (w_e + 1)。- 将两个组件
set1和set2统一起来。 - 从步骤
2中为下一个MST边缘e重复。
运行时间:O(log*log\V_x)。
如果问题变成:详细列出完整图的所有边e = (v1, v2)及其权重w,我们只需在步骤6和7之间做。
for all vertices v1 in set1
for all vertices v2 in set2
create edge e = (v1, v2); ignore if edge is the MST edge
w_e = w_mst_edge + 1因此,运行时间变成了O(x,E,x,n,2,2),因为我们在完整的图G中有一条维-E-x-1的G边。
https://stackoverflow.com/questions/27772118
复制相似问题

