Kruskal算法的运行时间
Kruskal的算法如下:
MST-KRUSKAL(G,w)
1. A={}
2. for each vertex v∈ G.V
3. MAKE-SET(v)
4. sort the edges of G.E into nondecreasing order by weight w
5. for each edge (u,v) ∈ G.E, taken in nondecreasing order by weight w
6. if FIND-SET(u)!=FIND-SET(v)
7. A=A U {(u,v)}
8. Union(u,v)
9. return A根据我的教科书:
在第1行初始化集合A需要O(1)时间,而在第4行中排序边的时间是O(E lgE)。第5-8行的for循环在不相交的集合林上执行O(E)、FIND-SET和UNION操作。同时,这些操作需要O(V+E)α(V))时间,其中α是一个增长非常慢的函数。因为我们假设G是连通的,所以我们的E_( <= _x_,我们有_此外,由于Kruskal算法的运行时间为O(LgV)=O( lgE),因此α(V)=O(LgE)算法的总运行时间为O(E LgE)。观察到|E|<|V|^2,我们得到了lg |E|=O( lgV),因此我们可以将Kruskal算法的运行时间重新描述为O(E LgV)。
你能解释一下为什么我们推断第4行的边排序的时间是O(E lgE)吗?另外,如何得到总时间复杂度为O((V+E)α(V))?
另外,假设图中的所有边权都是从1到x的整数。你能让Kruskal的算法运行多快?如果边权值是从1到W的整数,对于某些常数W,又会怎样呢?
时间复杂度如何取决于边的权重?
编辑:
另外,假设图中的所有边权都是从1到x的整数。你能让Kruskal的算法运行多快?
我想过以下几点:
为了使Kruskal算法运行得更快,我们可以使用计数排序对边缘进行排序。
- 第1行需要O(1)时间。
- 第2-3行需要O(v)时间.
- 第4行需要O(|V|+|E|)时间。
- 第5-8行需要O({##**$$}}E_α(_~_\_
- 第9行需要O(1)时间。
因此,如果使用计数排序来求解边,则Kruskal的时间复杂度将是
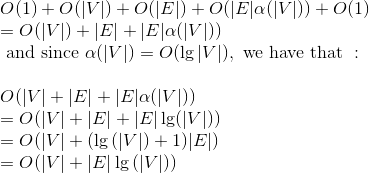
你能告诉我我的想法是否正确吗?
另外:
如果边权值是从1到W的整数,对于某些常数W,又会怎样呢?
我们将再次使用计数排序。算法将是相同的。我们发现时间的复杂性如下:
- 第1行需要O(1)时间。
- 第2-3行需要O( The )时间。
- 第4行要求O(W+|E|)=O(W)+O(x=E)=O(1)+O(x=E)=O(x=E)时间。
- 第5-8行需要O({##**$$}}E_α(_~_\_
- 第9行需要O(1)时间。
因此,时间复杂性将是:
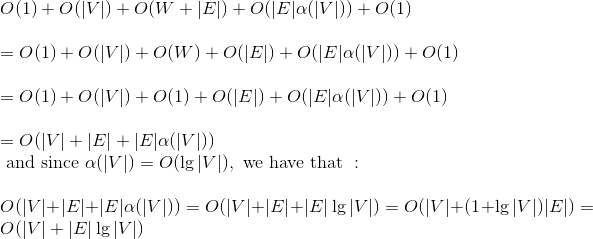
回答 1
Stack Overflow用户
发布于 2015-04-10 12:45:50
你能解释一下为什么我们推断第4行的边排序的时间是O(E*lgE)吗?
为了对一组N项进行排序,我们使用了O(N_lg(N))算法,即快速排序、合并排序或堆排序。因此,要排序E边,我们需要O(E_lg(E))时间。然而,在某些情况下,这是不必要的,因为我们可以使用复杂度更高的排序算法(进一步阅读)。
另外,如何得到总时间复杂度为O((V+E)α(V))?
我不认为总复杂度是O((V+E)α(V))。这就是5-8循环的复杂性。O((V+E)α(V))复杂度来自于V生成操作和E Union操作.为了找出为什么我们用α(V)来乘它,你需要阅读一些算法书中对不相交集数据结构的深入分析。
你能让Kruskal的算法运行多快?
对于第一部分,第4行,我们有O(E*lg(E))复杂度;对于第二部分,第5-8行,我们有O((E+V)_α(V))复杂度。这两种方法总结了O(E_lg(E))复杂度。如果我们使用O(N*lg(N))排序,这是无法改进的。
如果边权值是从1到W的整数,对于某些常数W,又会怎样呢?
如果是这样的话,那么我们可以使用第一部分的计数排序。给出了O(E+W) = O(E)的第4行复杂度。在这种情况下,算法的总复杂度为O((E+V)*α(V))。但请注意,在现实中O(E + W)包含一个常数,这个常数可能相当大,对于大W值可能是不切实际的。
时间复杂度如何取决于边的权重?
如前所述,如果边的权重足够小,我们可以使用计数排序和加速算法。
编辑: 另外,假设图中的所有边权都是从1到x的整数。你能让Kruskal的算法运行多快?我想过以下几点: 为了使Kruskal算法运行得更快,我们可以使用计数排序对边缘进行排序。 第1行需要O(1)时间。第2-3行需要O(vα( The ))时间。第4行需要O(|V|+|E|)时间。第5-8行需要O({##**$$}}E_α(_~_\_第9行需要O(1)时间。
您的想法是正确的,但您可以使边界更小。
第2-3行所需的是O( The ),而不是O({##**$$}}α(~##*}))。然而,在以前的计算中,我们将其简化为O({x}),使计算更容易。
有了这个,你得到的时间是: O(1) +O(x=1)+O(x=0)+O(x=0)+O(n=0)+0(x=0),E=0(x=1)+0(x=1)+O(x=1)+O(x=0,0,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,0,0
您可以将其简化为O(({##**$}})*α(\x~(-V),或者是O(\x~(2+))(x~*)(x~*)。
所以,尽管你是对的,但由于O(({##**$}})*α
的计算是类似的。
https://stackoverflow.com/questions/29561174
复制相似问题

