从左上角到右下角排序坐标
从左上角到右下角排序坐标
提问于 2015-04-14 14:29:46
如何尝试从左上角到右下角排列不规则数组的点,例如在下面的图像中?
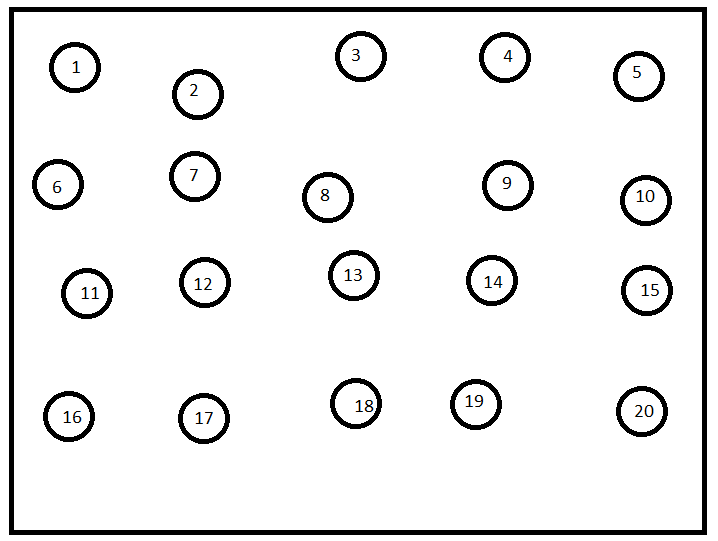
我考虑过的方法有:
- 计算每个点与图像左上角的距离(毕达哥拉斯定理),但在
Y坐标上应用某种加权,试图对同一“row”上的点排序,例如distance = SQRT((x * x) + (weighting * (y * y))) - 将点排序为逻辑行,然后对每一行进行排序。
部分困难在于,我不知道图像中会出现多少行和列,再加上点数组的不规则性。如有任何建议,将不胜感激。
回答 3
Stack Overflow用户
回答已采纳
发布于 2020-11-03 08:56:10
尽管这个问题比较老一些,但我最近在校准相机时遇到了类似的问题。
该算法非常简单,并且基于本论文。
- 找到左上角: min(x+y)
- 找到右上角:max(X)
- 从点创建一条直线。
- 计算所有点到直线的距离
- 如果它小于圆的半径(或阈值):点在顶部。
- 否则:点在块的其余部分。
- 按x值对上线的点进行排序并保存。
- 重复,直到没有剩下的点。
我的python实现如下所示:
#detect the keypoints
detector = cv2.SimpleBlobDetector_create(params)
keypoints = detector.detect(img)
img_with_keypoints = cv2.drawKeypoints(img, keypoints, np.array([]), (0, 0, 255),
cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
points = []
keypoints_to_search = keypoints[:]
while len(keypoints_to_search) > 0:
a = sorted(keypoints_to_search, key=lambda p: (p.pt[0]) + (p.pt[1]))[0] # find upper left point
b = sorted(keypoints_to_search, key=lambda p: (p.pt[0]) - (p.pt[1]))[-1] # find upper right point
cv2.line(img_with_keypoints, (int(a.pt[0]), int(a.pt[1])), (int(b.pt[0]), int(b.pt[1])), (255, 0, 0), 1)
# convert opencv keypoint to numpy 3d point
a = np.array([a.pt[0], a.pt[1], 0])
b = np.array([b.pt[0], b.pt[1], 0])
row_points = []
remaining_points = []
for k in keypoints_to_search:
p = np.array([k.pt[0], k.pt[1], 0])
d = k.size # diameter of the keypoint (might be a theshold)
dist = np.linalg.norm(np.cross(np.subtract(p, a), np.subtract(b, a))) / np.linalg.norm(b) # distance between keypoint and line a->b
if d/2 > dist:
row_points.append(k)
else:
remaining_points.append(k)
points.extend(sorted(row_points, key=lambda h: h.pt[0]))
keypoints_to_search = remaining_points
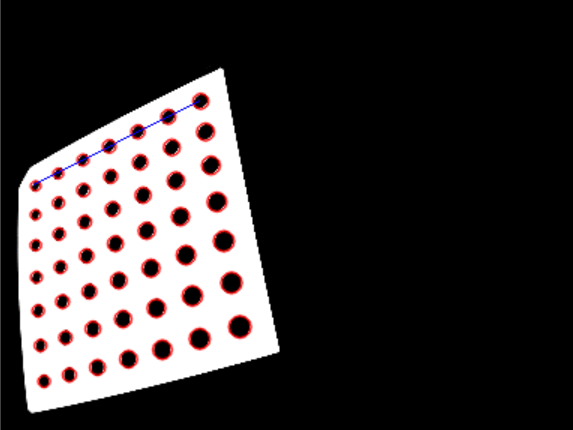
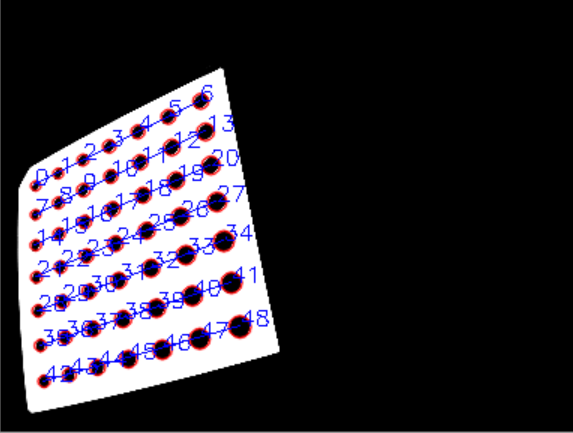
Stack Overflow用户
发布于 2021-04-07 03:10:40
跳到这个旧线程上,因为我刚刚处理了同样的事情:按从左到右,从上到下的位置对一个倾斜排列的放置对象网格进行排序。原始post顶部的绘图完美地总结了它,只不过此解决方案支持节点数目不同的行。
以上Vogt的脚本非常有用(下面的脚本完全基于他/她的脚本),但我的条件比较狭窄。Vogt的解决方案可以容纳一个可能从水平轴倾斜的网格。我假设没有倾斜,所以我不需要比较距离一个潜在倾斜的顶端线,而是从一个点的y值。
下面的Javascript:
interface Node {x: number; y: number; width:number; height:number;}
const sortedNodes = (nodeArray:Node[]) => {
let sortedNodes:Node[] = []; // this is the return value
let availableNodes = [...nodeArray]; // make copy of input array
while(availableNodes.length > 0){
// find y value of topmost node in availableNodes. (Change this to a reduce if you want.)
let minY = Number.MAX_SAFE_INTEGER;
for (const node of availableNodes){
minY = Math.min(minY, node.y)
}
// find nodes in top row: assume a node is in the top row when its distance from minY
// is less than its height
const topRow:Node[] = [];
const otherRows:Node[] = [];
for (const node of availableNodes){
if (Math.abs(minY - node.y) <= node.height){
topRow.push(node);
} else {
otherRows.push(node);
}
}
topRow.sort((a,b) => a.x - b.x); // we have the top row: sort it by x
sortedNodes = [...sortedNodes,...topRow] // append nodes in row to sorted nodes
availableNodes = [...otherRows] // update available nodes to exclude handled rows
}
return sortedNodes;
};以上假设所有节点高度相同。如果有些节点比其他节点高得多,则获取所有节点的最小节点高度的值,并使用它代替迭代的"node.height“值。也就是说,您将修改上面脚本的这一行,以使用所有节点的最小高度,而不是迭代的节点。
if (Math.abs(minY - node.y) <= node.height)Stack Overflow用户
发布于 2015-04-14 15:02:57
我提出以下意见:
- 点数(p)
- 对于每一点,它都是x和y坐标,直到某个数,比如
如果m,n太大,计数数就会下降。迭代地确定m,n,这样
p点的数目就会保持不变。
起始值可以与max(x) - min(x)保持一致。对于搜索,请使用二进制搜索。X和Y尺度是相互独立的。
用自然的话来说,这将通过拉伸或缩小网格距离将单个点固定到网格点,直到所有点最多有一个公共坐标(X或Y),但没有2个点重叠。你也可以称之为分类。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/29630052
复制相关文章
相似问题

