matplotlib (mplot3d) --如何在三维图形中增加轴(拉伸)的大小？
matplotlib (mplot3d) --如何在三维图形中增加轴(拉伸)的大小？
提问于 2015-05-13 18:58:38
到目前为止，我有这样的看法：
x,y,z = data.nonzero()
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, zdir='z', c= 'red')
plt.savefig("plot.png")这就产生了：
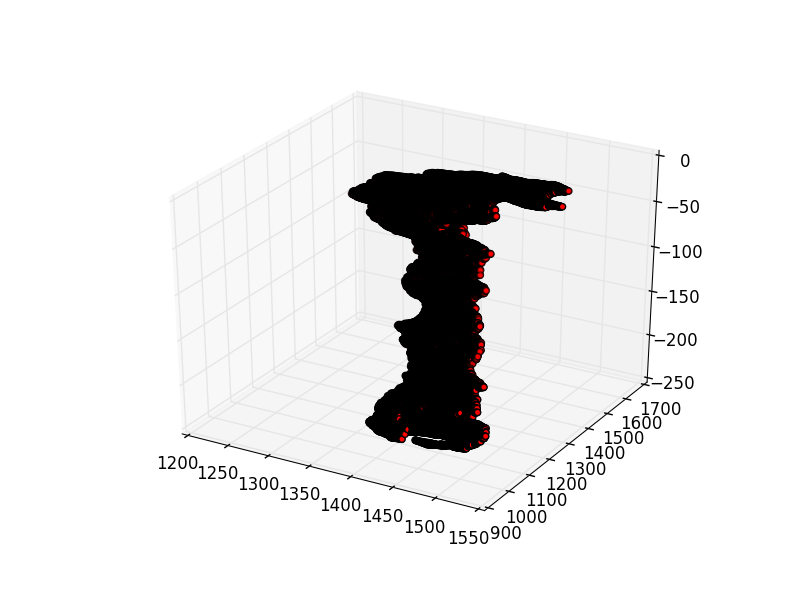
我想做的是把它拉出来，使Z轴高9倍，并保持X和Y不变。不过我想保持相同的坐标。
到目前为止我试过这个人：
fig = plt.figure(figsize=(4.,35.))但这只是延伸了plot.png的图像。
回答 7
Stack Overflow用户
回答已采纳
发布于 2015-05-19 18:59:47
下面的代码示例提供了一种相对于其他轴缩放每个轴的方法。但是，要做到这一点，您需要修改Axes3D.get_proj函数。下面是基于matplot：toolkits/mplot3d/tutorial.html#line-plots提供的示例的一个示例
(答案末尾有一个较短的版本)
from mpl_toolkits.mplot3d.axes3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
#Make sure these are floating point values:
scale_x = 1.0
scale_y = 2.0
scale_z = 3.0
#Axes are scaled down to fit in scene
max_scale=max(scale_x, scale_y, scale_z)
scale_x=scale_x/max_scale
scale_y=scale_y/max_scale
scale_z=scale_z/max_scale
#Create scaling matrix
scale = np.array([[scale_x,0,0,0],
[0,scale_y,0,0],
[0,0,scale_z,0],
[0,0,0,1]])
print scale
def get_proj_scale(self):
"""
Create the projection matrix from the current viewing position.
elev stores the elevation angle in the z plane
azim stores the azimuth angle in the x,y plane
dist is the distance of the eye viewing point from the object
point.
"""
relev, razim = np.pi * self.elev/180, np.pi * self.azim/180
xmin, xmax = self.get_xlim3d()
ymin, ymax = self.get_ylim3d()
zmin, zmax = self.get_zlim3d()
# transform to uniform world coordinates 0-1.0,0-1.0,0-1.0
worldM = proj3d.world_transformation(
xmin, xmax,
ymin, ymax,
zmin, zmax)
# look into the middle of the new coordinates
R = np.array([0.5, 0.5, 0.5])
xp = R[0] + np.cos(razim) * np.cos(relev) * self.dist
yp = R[1] + np.sin(razim) * np.cos(relev) * self.dist
zp = R[2] + np.sin(relev) * self.dist
E = np.array((xp, yp, zp))
self.eye = E
self.vvec = R - E
self.vvec = self.vvec / proj3d.mod(self.vvec)
if abs(relev) > np.pi/2:
# upside down
V = np.array((0, 0, -1))
else:
V = np.array((0, 0, 1))
zfront, zback = -self.dist, self.dist
viewM = proj3d.view_transformation(E, R, V)
perspM = proj3d.persp_transformation(zfront, zback)
M0 = np.dot(viewM, worldM)
M = np.dot(perspM, M0)
return np.dot(M, scale);
Axes3D.get_proj=get_proj_scale
"""
You need to include all the code above.
From here on you should be able to plot as usual.
"""
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure(figsize=(5,5))
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
ax.plot(x, y, z, label='parametric curve')
ax.legend()
plt.show()标准产出：
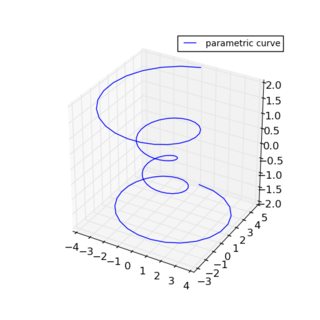
按(1、2、3)缩放：
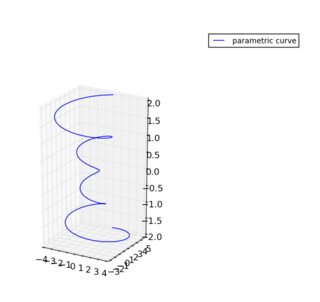
按(1、1、3)缩放：
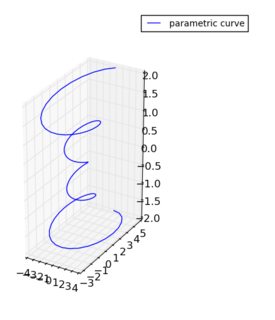
我特别喜欢这种方法的原因是，交换z和x，按(3，1，1)进行缩放：
下面是代码的较短版本。
from mpl_toolkits.mplot3d.axes3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure(figsize=(5,5))
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
"""
Scaling is done from here...
"""
x_scale=1
y_scale=1
z_scale=2
scale=np.diag([x_scale, y_scale, z_scale, 1.0])
scale=scale*(1.0/scale.max())
scale[3,3]=1.0
def short_proj():
return np.dot(Axes3D.get_proj(ax), scale)
ax.get_proj=short_proj
"""
to here
"""
ax.plot(z, y, x, label='parametric curve')
ax.legend()
plt.show()Stack Overflow用户
发布于 2015-05-24 01:33:57
请注意，下面的答案简化了补丁程序，但使用了与@ChristianSarofeen.的答案相同的基本原则。
解决方案
正如在其他答案中已经指出的，它不是目前在matplotlib中实现的特性。但是，由于您所要求的只是一个3D转换，它可以应用于matplotlib所使用的现有投影矩阵，而且由于的出色特性，这个问题可以通过一个简单的oneliner来解决。
ax.get_proj = lambda: np.dot(Axes3D.get_proj(ax), np.diag([scale_x, scale_y, scale_z, 1]))其中，scale_x、scale_y和scale_z是从0到1的值，它们将相应地沿着每个轴重新缩放您的地块。ax就是ax = fig.gca(projection='3d')可以得到的三维轴。
解释
为了解释，函数get_proj of Axes3D从当前观看位置生成投影矩阵。将其乘以一个缩放矩阵：
scale_x, 0, 0
0, scale_y, 0
0, 0, scale_z
0, 0, 1包括缩放到渲染器使用的投影。所以，我们在这里做的是用一个表达式替换原始的get_proj函数，这个表达式接受原始get_proj的结果，然后乘以缩放矩阵。
示例
为了用标准参数函数示例说明结果：
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z ** 2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
# OUR ONE LINER ADDED HERE:
ax.get_proj = lambda: np.dot(Axes3D.get_proj(ax), np.diag([0.5, 0.5, 1, 1]))
ax.plot(x, y, z)
plt.show()对于值0.5, 0.5, 1，我们得到：
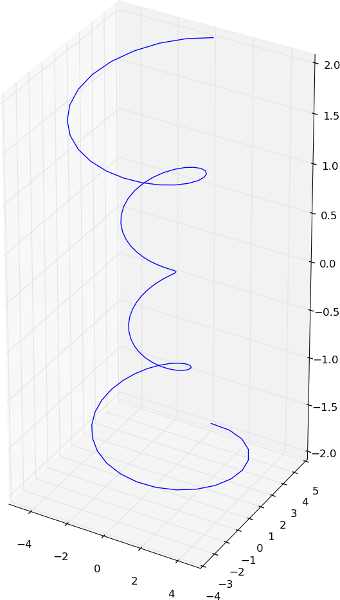
而对于值0.2, 1.0, 0.2，我们得到：
Stack Overflow用户
发布于 2021-07-23 14:29:15
在我的例子中，我想要拉伸z轴2次，以获得更好的点能见度。
from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
# plt.rcParams["figure.figsize"] = (10,200)
# plt.rcParams["figure.autolayout"] = True
ax = plt.axes(projection='3d')
ax.set_box_aspect(aspect = (1,1,2))
ax.plot(dataX,dataY,dataZ)页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接：
https://stackoverflow.com/questions/30223161
复制相关文章
相似问题
腾讯云开发者
