问将4个协调连接在一起的算法，使其总是产生四边形。

EN

在几个阶段中，假设最终结果需要4对点(和/或它们之间的直线方程)：

1. 取任何三个点，然后形成一个三角形。
2. 如果第四个点在套路内，则将其与三个中的ny交换。
3. 只剩下最后一个点，计算出你想把它附加到哪两个点。这是通过播放线方程和找到相交点的位置来完成的。下文对此作出澄清。
4. 返回三角形的两边+第四点和第二阶段中选择的两条线。

第2步澄清：

让我们说，A点不是在三角形(即BCD)中。每条线都把平原分成两面。我们想找出点(B，C或D) s.t。它和A之间的线是在另外两条线之间运行的(它们在两条线的对立面)。这就是我们不想附加在A上的一点。

例子:给定A(0,0)，B(10,0)，C(10,10)和D(0,10)。我们有三角BCD。BC线在平原的同一侧离开A&D。DC也是。线路AC离开B&D在平原的对面，所以我们想连接A和B& C。

考虑通过绘制前三个点定义的三条线来划分平面。它界定了7个区域。通过三个符号区域测试(三角形的代数面积ABD、BCD、CAD)，您可以很容易地找到第四个点属于哪个区域。

在每一种情况下绘制一个四边形是很简单的(每个案例可以有一个、两个或三个解决方案)。

在下面的例子中，使用区域-++中的D，ADBC就可以了。

​

​

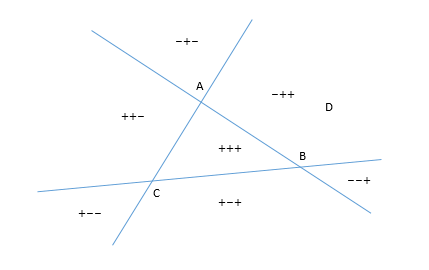
实际上，两个区域评估就足够了:如果第一个测试返回- (regions -+-，-++或--+)，则ADBC是一个解决方案，如果第二个测试返回- (Regions+-+或+--)，则ABDC是一个解决方案，否则(Regions++-或+++)是一个解决方案。

考虑仿射变换

Px = Ax + u (Bx - Ax) + v (Cx - Ax)
Py = Ay + u (By - Ay) + v (Cy - Ay)

它将(0, 0)映射到A，(1, 0)映射到B，(0, 1)映射到C。(这将三角形ABC置于标准位置。)

求解2x2线性系统

Dx = Ax + u (Bx - Ax) + v (Cx - Ax)
Dy = Ay + u (By - Ay) + v (Cy - Ay)

给出与(u, v)对应的D值。

然后,

if u < 0 => ABCD
else if v < 0 => BCAD
else => CABD

得到的四边形与三角形ABC具有相同的方向。

​

​