我的fourier级数不适合这个图
我的fourier级数不适合这个图
提问于 2015-05-26 01:59:25
我试图绘制一个傅里叶级数,它应该符合原始图(这是正确的),但我不知道哪里出了问题。我还复核了傅里叶近似。
生成原始图时:
t=-pi:0.01:0;
x=ones(size(t));
plot(t,x)
axis([-3*pi 3*pi -1 4])
hold on
t=0:0.01:pi;
y=cos(t);
plot(t,y)而傅里叶级数是用以下方式产生的:
t=-pi:0.01:pi;
f=1/2;
for n=1:5
costerm=0;
if n/2== round(n/2)
sinterm=((-2*n)/(pi*(1-n^2)))*sin(2*n*t);
else
sinterm= (-2/(pi*n))*sin(2*n*t);
end
f=f+sinterm+costerm;
end
plot(t,f)图如下所示:

有人能告诉我为什么这不管用吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2015-05-26 14:18:42
首先需要注意的是,在您的绘图中生成的系列在支持间隔[-pi:pi]中运行了两个阶段。这指向sin(2*n*t)参数中的一个不正确的常量,它应该是sin(n*t)。
此外,作为一般规则
- 奇数函数只有
sin项 - 甚至函数都只有
cos项 - 否则,Fourier级数包含
sin和cos项的混合物。
在您的示例中,函数既不是偶数,也不是奇数,因此您应该希望同时出现sin和cos术语。但是,您只需要计算sinterm并离开costerm=0。更具体地说,虽然余弦级数系数对所有n>1计算为0,但实际上忽略了n=1的术语,即0.5*cos(t)。
有了这些修正,你应该得到
f=1/2 + 0.5*cos(t);
for n=1:5
if 0==mod(n,2)
sinterm=((-2*n)/(pi*(1-n^2)))*sin(n*t);
else
sinterm= (-2/(pi*n))*sin(n*t);
end
f=f+sinterm;
end它应该给出如下的图(蓝线是原始函数,红线是Fourier级数展开):
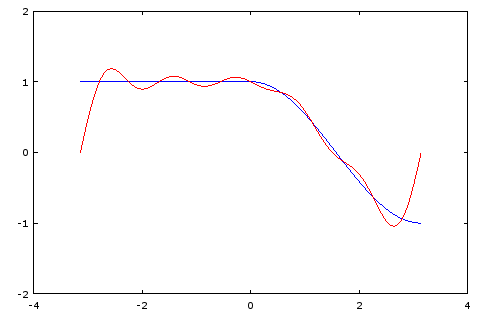
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/30448275
复制相关文章
相似问题

