是否有一种标准的C方法来“完美地”打印浮点值la Dragon4?
阅读http://web.archive.org/web/20150330014345/http://www.serpentine.com/blog/2011/06/29/here-be-dragons-advances-in-problems-you-didnt-even-know-you-had/时,我注意到他们将新算法与glibc的printf中的算法进行了比较
Grisu3比printf在GNU libc中使用的算法快5倍。
但与此同时,我没有为printf找到任何格式说明符,这将自动找到要打印的最佳小数位数。我所有的尝试都有一些奇怪的默认值,比如%f小数点后的6位,%g的2点,%e的6点。
我如何实际使用本文中提到的glibc中的算法实现?在glibc中是否真的有这样的实现,标准中是否以任何方式进行了讨论?
回答 2
Stack Overflow用户
发布于 2015-06-03 11:46:11
这是真正的文章。博客文章指的是第7节中的结果(换句话说,“他们”不是在比较博客文章中的任何内容,“他们”是在回溯实际文章中的信息,忽略了关键的细节):
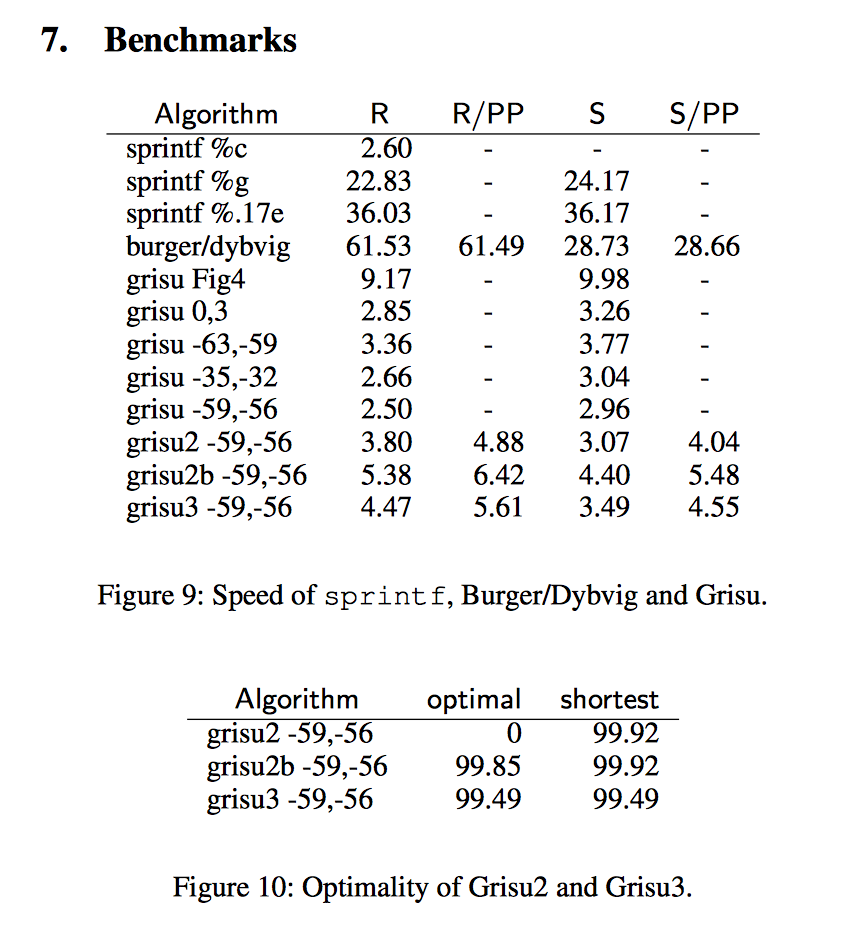
Dragon4或Grisu3的实现可以在现代编程语言的实现中找到,这些语言指定这种“最小小数位数”的方式(我建议您避免称它为“完美的”)。Java在某些上下文中使用这种类型的十进制转换,Ruby也是如此。C不是指定将“最小小数位数”转换为十进制的语言之一,因此编译器或libc没有理由为Dragon4或Grisu3提供实现。
Stack Overflow用户
发布于 2015-06-03 11:06:13
没有所谓的“最佳小数位数”,因为浮点数不是以小数的形式存储的。所以你需要定义什么是“最好”。如果要打印数字而不丢失任何可能的信息,C11将为您提供格式说明符%a (不包括未指定行为的非规范化浮点数)。
C11标准的默认值是%f和%e的6位数字,而%g的默认值是:
如果不为零,则P等于精度;如果省略精度,则等于6;如果精度为零,则等于1。然后,如果E型转换的指数为X:-如果P>X≥−4,则转换为类型f(或F)和精度P−(X + 1)。-否则,转换的样式为e(或E),精度为P−1。
如果要使用该算法,请为其实现自己的函数。或者希望glibc在过去的5年里已经实施了。或者重新考虑打印浮点数的性能是否真的是一个问题。
https://stackoverflow.com/questions/30617131
复制相似问题

