稀疏矩阵生成的复杂性
稀疏矩阵生成的复杂性
提问于 2015-06-16 16:25:49
我有一个对称矩阵S(n*n),其中大约70%的数据是0。
对称矩阵
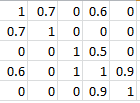
我想把对称矩阵转换成有t行的稀疏矩阵。
从原始对称矩阵生成稀疏矩阵的时间复杂度是多少?
它是O(n^2)吗,因为我必须遍历每一行/列的交集,并得到不是0的元素?
由于我处理的是对称矩阵,我可以说我的时间复杂度可以降低到O((n*(n+1))/2),因为在对称矩阵ai= aj中?在这种情况下,如果遇到ai为0,我可以说是aj=0。这可以使我的循环减少大约一半。
回答 1
Stack Overflow用户
回答已采纳
发布于 2015-06-16 16:40:23
当将对称矩阵的完整表示转换为稀疏表示时,需要扫描主对角线及以上(或主对角线及以下)上的所有元素。对于( n )矩阵矩阵,这是需要扫描的(n^2+n)/2条目。因此,您需要执行O(n^2)工作,以确定需要输入到稀疏矩阵中的内容。
在构造稀疏矩阵时,需要将原始矩阵中的所有非空项存储到稀疏矩阵中。对于0矩阵,这不需要额外的工作,对于完全密集的矩阵,这需要(n^2+n)/2插入操作。
因此,从对称矩阵转换到稀疏表示总是需要O(n^2)时间--实际上需要Theta(n^2)时间。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/30873142
复制相关文章
相似问题

