问右手欧拉角XYZ到左撇子欧拉角XYZ

EN

记数法：

x,y,z - old system basis
x',y',z' - new system basis

Transformation between systems:
x' = x
y' = y
z' = -z

Euler angles:
EulerXYZ = (alfa,beta,gamma)
EulerXYZ' = (alfa',beta',gamma') = ?

现在我想出两种方法来解决这个问题：

图形化

1. 绘制这两种系统
2. 使用右手规则在右撇子上标记正旋转。
3. 用左手规则在左撇子上做正旋转。
4. 当相应轴上的旋转一致时，则转换为angle' = angle，否则为angle' = -angle。

​

​

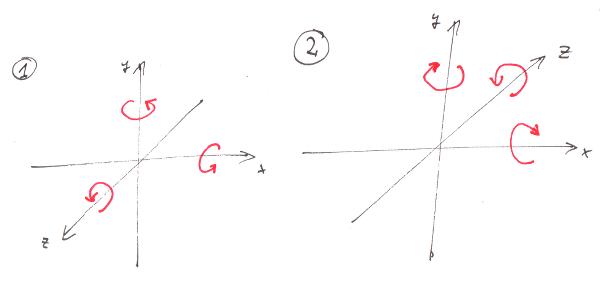
在上面的图片中，#1是右撇子，#2是左手系统(红线总是经过黑线)。

看看这张照片，我们可以得出结论：alfa',beta',gamma' = -alfa,-beta,+gamma

代数法

转换可以用几何代数来计算。它在某种程度上类似于四元数，但旋转发生在“定向平面”，而不是“圆轴”。

有向平面是由两个向量u^v的乘积定义的，具有以下性质：-(u^v) = (-u)^v = u^(-v)

旋转由转子R(angle, plane)和R(angle, -plane) = R(-angle, plane)定义。

现在：

R(alfa, y^z) = R(-alfa, -(y^z)) = R(-alfa, y^(-z)) = R(-alfa, y'^z')
R(beta, x^z) = R(-beta, x'^z')
R(gamma, x^y) = R(+gamma, x'^y')

所以

alfa',beta',gamma' = -alfa,-beta,+gamma