问用Direct2D绘制样条

EN

除非您已经有基本NURBS操作的工作代码，或者您是NURBS专家，否则我建议您使用一些NURBS库。通常，与您的问题相关的操作集合是:点评估、节点插入、分裂，以及可能的程度提升。

作为一般性，我将描述三种可能的解决方案。

结裂

假设您输入的NURBS曲线是非有理的(没有权值=单位权重)，并且它们的度不能超过所得到的Bezier曲线的最大允许度。然后样条的每个跨度都是一条多项式曲线，因此可以提取为Bezier曲线。

根据您使用的库，算法的描述可能有所不同。以下是可能的变体：

1. 如果有一个函数将NURBS曲线分割成Bezier曲线，只需调用它。
2. 假设在给定的参数下，有一个将曲线分割成两个子曲线的函数。然后将你的曲线分裂成任何内部结(即不等于最小/最大节)。对每个子曲线做同样的操作，直到没有内部结，这意味着所有的曲线都是Bezier。
3. 任何NURBS库都必须具有节点插入功能。对于每个多重度小于D(度)的节点Ki，用param = Ki调用节点插入。您可以按任何顺序插入不同的结。库还可以包含“多个节点插入”，这允许将所有插入合并到一个调用中。最后，最小/最大节点必须具有多重性D+1，所有内部节点必须具有多重性D。此时控制点充分描述了所需的Bezier曲线:控制点0 . D定义0- Bezier，D. 2D定义第1- Bezier，.，q.(q+1) D控制点定义了q-th Bezier.

如果输入NURBS曲线的程度低于Bezier曲线所需的程度，您也可以对原始NURBS曲线或由此产生的Bezier曲线调用度提升。说到ID2D1GeometrySink，它接受所有<= 3度的贝塞尔曲线(线性贝塞尔曲线只是一个线段)，所以它是不必要的。

如果你的NURBS曲线可能有不可接受的高度，或者是理性的，那么你必须用三次样条(更难更快)或者用折线(更简单但更慢)来逼近这条曲线。

保折线逼近

这里是一个相当简单的递归算法，它建立了具有保证误差<= MaxErr的NURBS曲线的折线逼近。

1. 从曲线的第一个控制点到最后一个控制点画一个线段。
2. 检查是否所有控制点都在离段的MaxErr距离之内。
3. 如果是，则将线段添加到输出中。
4. 否则，将中间的曲线分割成两个子曲线，并递归地逼近它们。

要实现它，您需要NURBS曲线分割操作(可以通过节点插入实现)。

启发式折线逼近

如果没有NURBS库在手边，实施结插入可能会造成很大的痛苦。这就是为什么我描述了另一个解决方案，它只使用NURBS曲线的点评估。您可以通过de算法或定义实现点计算(请参阅基函数和NURBS曲线定义)

该算法是递归的，它接受原始曲线上的一个参数区间作为输入。

1. 评估参数区间的起始点和终点。
2. 画一条线段穿过它们。
3. 求出参数区间内曲线上的若干点。
4. 检查这些内部点是否在线段的MaxErr距离内。
5. 如果是，则将线段添加到输出中。
6. 否则，将参数区间分成两半，然后递归地调用它们的逼近。

该算法是自适应的，在一些罕见的情况下，在实际应用中会产生很差的逼近效果。检查点可以在参数区间内均匀选择。为了获得更高的可靠性，在参数区间内的输入曲线的所有节点处也要对曲线进行评估。

第三方图书馆

如果您不打算经常使用NURBS，我建议您使用锡样条库。它是非常小的设计，没有依赖，并拥有麻省理工学院的许可。而且，它似乎是积极开发的，因此您可以在遇到任何问题时与作者进行交流。

似乎第一种解决方案对主题启动器来说已经足够了，下面是用微小样条将NURBS分割成Bezier曲线的代码：

#include <stdlib.h>
#include <stdio.h>
#include <assert.h>
#include <math.h>
#include "tinysplinecpp.h"
#include "debugging.h"

int main() {
    //create B-spline curve and set its data
    TsBSpline nurbs(3, 2, 10, TS_NONE);
    float knotsData[] = {0.0f, 0.0f, 0.0f, 0.0f, 0.3f, 0.3f, 0.5f, 0.7f, 0.7f, 0.7f, 1.0f, 1.0f, 1.0f, 1.0f};
    for (int i = 0; i < nurbs.nKnots(); i++)
        nurbs.knots()[i] = knotsData[i];
    for (int i = 0; i < nurbs.nCtrlp(); i++) {
        nurbs.ctrlp()[2*i+0] = 0.0f + i;
        float x = 1.0f - i / float(nurbs.nCtrlp());
        nurbs.ctrlp()[2*i+1] = x * x * x;
    }
    ts_bspline_print(nurbs.data());

    //insert knots into B-spline so that it becomes a sequence of bezier curves
    TsBSpline beziers = nurbs;
    beziers.toBeziers();
    ts_bspline_print(beziers.data());

    //check that the library does not fail us
    for (int i = 0; i < 10000; i++) {
        float t = float(rand()) / RAND_MAX;
        float *pRes1 = nurbs(t).result();
        float *pRes2 = beziers(t).result();
        float diff = hypotf(pRes1[0] - pRes2[0], pRes1[1] - pRes2[1]);
        if (diff >= 1e-6f)
            printf("Bad eval at %f: err = %f  (%f;%f) vs (%f;%f)\n", t, diff, pRes1[0], pRes1[1], pRes2[0], pRes2[1]);
    }

    //extract bezier curves
    assert(beziers.nCtrlp() % nurbs.order() == 0);
    int n = beziers.nCtrlp() / nurbs.order();
    int sz = nurbs.order() * 2; //floats per bezier
    for (int i = 0; i < n; i++) {
        float *begin = beziers.ctrlp() + sz * i;
        float *end = beziers.ctrlp() + sz * (i + 1);
        //[begin..end) contains control points of i-th bezier curve
    }

    return 0;
}

最后注

以上大多数文本都假设NURBS曲线是夹紧的，这意味着最小和最大节点具有多重D+1，有时也使用无夹紧NURBS曲线。如果您遇到一个，您还可能需要通过使用库的批准功能来夹紧它。方法toBeziers来自锡样条使用以上夹紧NURBS自动，您不需要手动夹紧它。

更清楚的是，ID2D1GeometrySink，不支持样条，而支持三次bezier曲线，这些曲线可以组合成样条。相反，你可以从你的样条数据中得到b-曲线，然后把它们添加到你的几何中。

这张图片简单地解释了该算法：

。

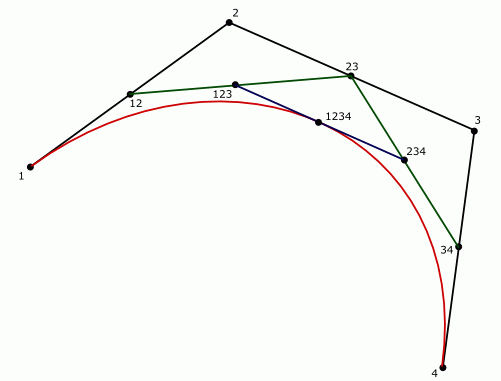
一篇简短和很好的解释的文章可以找到这里。你可以分裂你的样条，直到控制点重叠，程度可以降低，甚至直到所有的曲线都是平到成线为止。最后一件事并不是个坏主意，因为你的硬件不知道曲线，所以你通过的曲线会被转换成线条。当 you 执行此转换时，您可以确定平面度的公差，并避免难看的边缘。

我使用这个示例代码将基数样条转换为三次bezier补丁列表：http://www.codeproject.com/Articles/31859/Draw-a-Smooth-Curve-through-a-Set-of-D-Points-wit

它是为WPF编写的，但是由于WPF和Direct2D的编程模型不同(声明式和命令式)，所以很容易转换为Direct2D。