只沿一个轴平滑二维阵列
我想知道是否有人能帮助我将SciPy食谱中的平滑示例扩展到2D问题。
这个脚本对于平滑一维函数非常有用,它们也给出了在两个轴上进行二维平滑(即模糊图像)的代码。
但是,我想将这个函数应用于一个2D数据集,但只沿一个轴(x方向)。我可以在一个循环中这样做,通过检查y中的每个切片,应用一维卷积,然后重建数组。但这似乎是糟糕的编码技术。
因此,我想知道如何在2D中实现它?我想我需要制作一个只沿一个方向变化权重的2D内核,但我不知道如何做到这一点,也不知道应该使用哪个卷积函数(numpy.convolve、scipy.signal.convolve、scipy.ndimage.filters.convolve1d等)。
回答 2
Stack Overflow用户
发布于 2015-08-22 15:22:21
也许最简单的选择是在scipy.ndimage.filters中使用一维过滤器之一
from scipy import ndimage
from scipy.misc import lena
img = lena()
# a uniform (boxcar) filter with a width of 50
boxcar = ndimage.uniform_filter1d(img, 50, 1)
# a Gaussian filter with a standard deviation of 10
gauss = ndimage.gaussian_filter1d(img, 10, 1)您也可以使用非一维版本的过滤器,如:ndimage.gaussian_filter(img, (0, 10)) (即,设置过滤器宽度为0的轴线,您不希望顺利进行)。
要使任意内核平滑,可以使用scipy.ndimage.convolve1d
import numpy as np
kern = np.hanning(50) # a Hanning window with width 50
kern /= kern.sum() # normalize the kernel weights to sum to 1
hanning = ndimage.convolve1d(img, kern, 1)以下是各种输出的样子:
from matplotlib import pyplot as plt
fig, ax = plt.subplots(2, 2, figsize=(8, 8))
ax[0, 0].imshow(img)
ax[0, 0].set_title('Original')
ax[0, 1].imshow(boxcar)
ax[0, 1].set_title('Boxcar filter (width = 50)')
ax[1, 0].imshow(gauss)
ax[1, 0].set_title(r'Gaussian filter ($\sigma$ = 10)')
ax[1, 1].imshow(hanning)
ax[1, 1].set_title(r'Hanning window (width = 50)')
for aa in ax.flat:
aa.set_axis_off()
fig.tight_layout()
plt.show()

Stack Overflow用户
发布于 2015-08-22 15:13:39
引言
似乎您应该能够做ny=1来执行2D图像的一维卷积,但这表明食谱函数实际上使用的是长度2 * n + 1内核。这使我认为您可以使用ny=0,但这会在内核的定义中创建一个0/0。所以,那里也没有运气。:(基于此,我认为食谱对你的目的不太好,所以我提供了一种替代的方法来做你要求的事情。)
要执行二维阵列的平滑,只需沿一维卷积,只需制作一个二维阵列(核),其形状为1,
import numpy as np
kern = np.ones((11, 1)) # This will smooth along columns并将其正常化,使之归为一种,
kern /= kern.sum()然后用你的信号把它转过来,
import scipy.signal as signal
X, Y = np.mgrid[-70:70, -70:70]
Z = np.cos((X**2+Y**2)/200.) + np.random.normal(size=X.shape)
Z_smooth = signal.convolve(Z, kern)这应该会给你这样的东西,
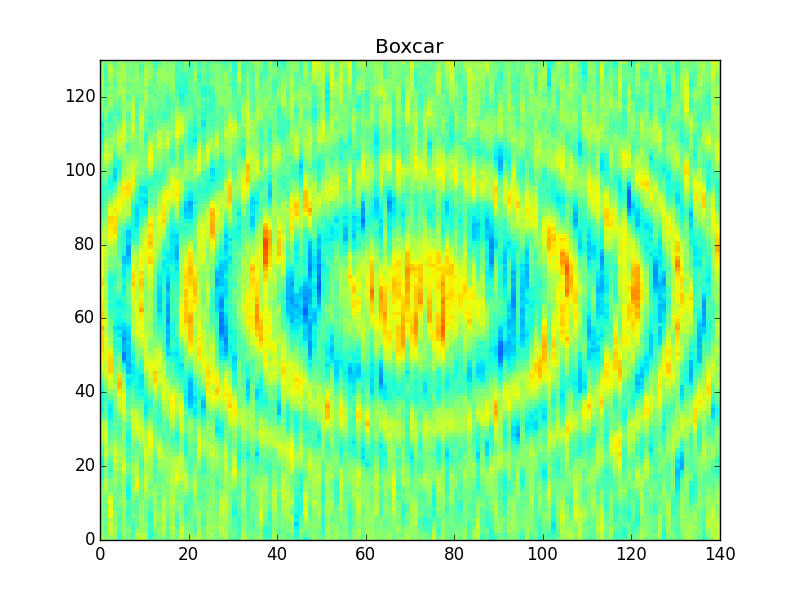
一个更好的内核
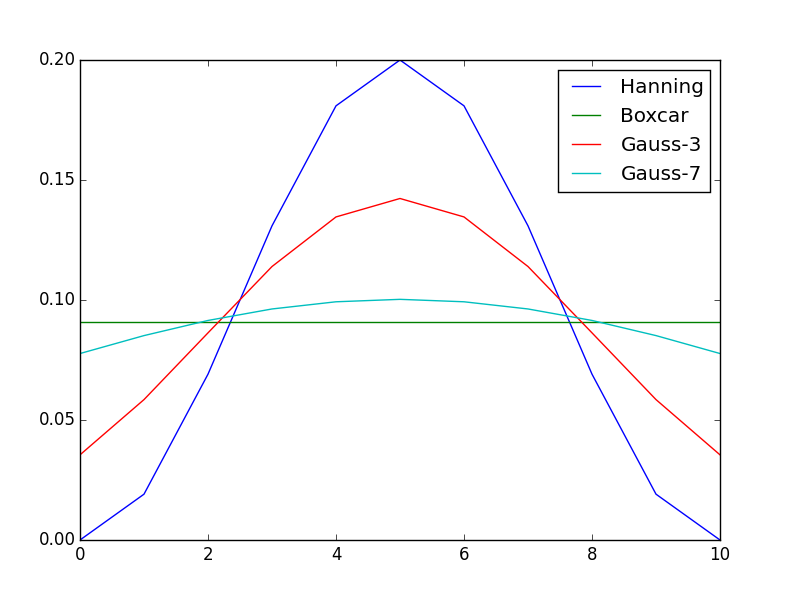
上面我使用了“boxcar”内核(常量值),很多人认为这个内核有点粗糙。人们通常更喜欢使用更锐利或更平滑的过滤器(例如,“汉宁”或“高斯”,如食谱中的那样)。
kern_hanning = signal.hanning(11)[:, None]
kern_hanning /= kern_hanning.sum()
kern_gauss7 = signal.gaussian(11, 7)[:, None]
kern_gauss7 /= kern_gauss7.sum()
kern_gauss3 = signal.gaussian(11, 3)[:, None]
kern_gauss3 /= kern_gauss3.sum()这些不同的窗户是这样的,
在应用这些过滤器之后,你会得到一些类似的信息,
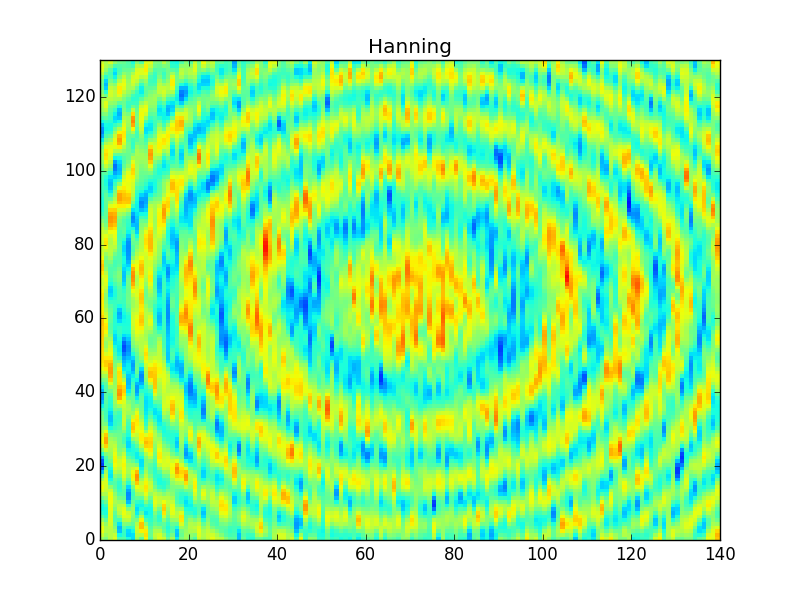
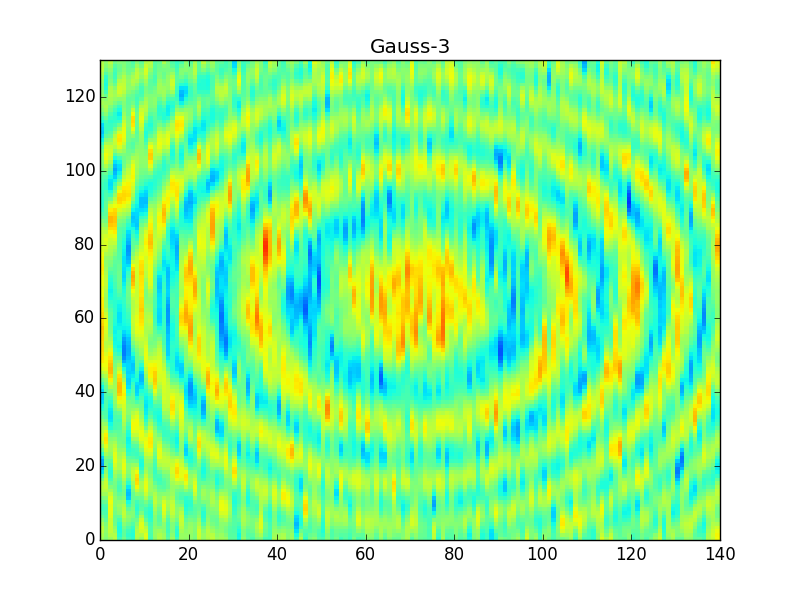
请注意,“Gauss7”内核与boxcar几乎相同,因此它在输出中产生非常相似的结果。另一方面,汉宁的窗口要细得多,因此它产生了一个更清晰的数据过滤器(更不用说在圆环上涂抹了)。
https://stackoverflow.com/questions/32155488
复制相似问题

