问破解编码采访，第6版，2.8

EN

您的解决方案是O(n^2) time ( ArrayList中的每个contains()都是O(n) time)和O(n)空间(用于存储nodeStorage)，而“更复杂”的解决方案是O(n)时间和O(1)空间。

这本书向任何感兴趣的人提供了以下解决方案，即O(n) time和O(1)空间：

如果我们移动两个指针，一个是速度1，另一个是速度2，如果链表有一个循环，它们就会相遇。为什么？想想两辆在一条赛道上行驶的汽车--越快越好，越慢越好！这里棘手的部分是找到循环的开始。想象一下，作为一个比喻，两个人绕着一条赛道跑，一个跑得比另一个快两倍。如果他们从同一个地方出发，他们下一次见面是什么时候？他们将在下一圈开始时见面。现在，让我们假设快跑者在n步跑圈上领先k米。他们下次什么时候见面？他们将在下一圈开始前遇到k米。(为什么？快跑者会做k+ 2(n - k)步，包括它的先头开始，慢跑者会做n-k步。这两个步骤都是循环开始前的k步。现在，回到问题，当快速运行程序( n2 )和慢速运行程序( n1 )在循环链接列表中移动时，当n1进入时，n2将在循环中占据先机。具体来说，它将具有k的先头，其中k是循环之前的节点数。因为n2有k个节点的先头，所以n1和n2会在循环开始之前遇到k个节点。因此，我们现在知道如下: 1. Head是来自LoopStart的k个节点(根据定义)。2. MeetingPoint for n1和n2是来自LoopStart的k个节点(如上面所示)。因此，如果我们将n1移回头部，并将n2保持在MeetingPoint，并以相同的速度移动它们，它们将在LoopStart相遇。

LinkedListNode FindBeginning(LinkedListNode head) {
   LinkedListNode n1 = head;
   LinkedListNode n2 = head;

   // Find meeting point
   while (n2.next != null) {
      n1 = n1.next;
      n2 = n2.next.next;
      if (n1 == n2) {
         break;
      }
   }
// Error check - there is no meeting point, and therefore no loop
   if (n2.next == null) {
      return null;
   }
   /* Move n1 to Head. Keep n2 at Meeting Point. Each are k steps
   /* from the Loop Start. If they move at the same pace, they must
   * meet at Loop Start. */
   n1 = head;
   while (n1 != n2) {
      n1 = n1.next;
      n2 = n2.next;
   }
   // Now n2 points to the start of the loop.
   return n2;
   }

我很难想象这个算法是怎么回事。希望这能帮到别人。

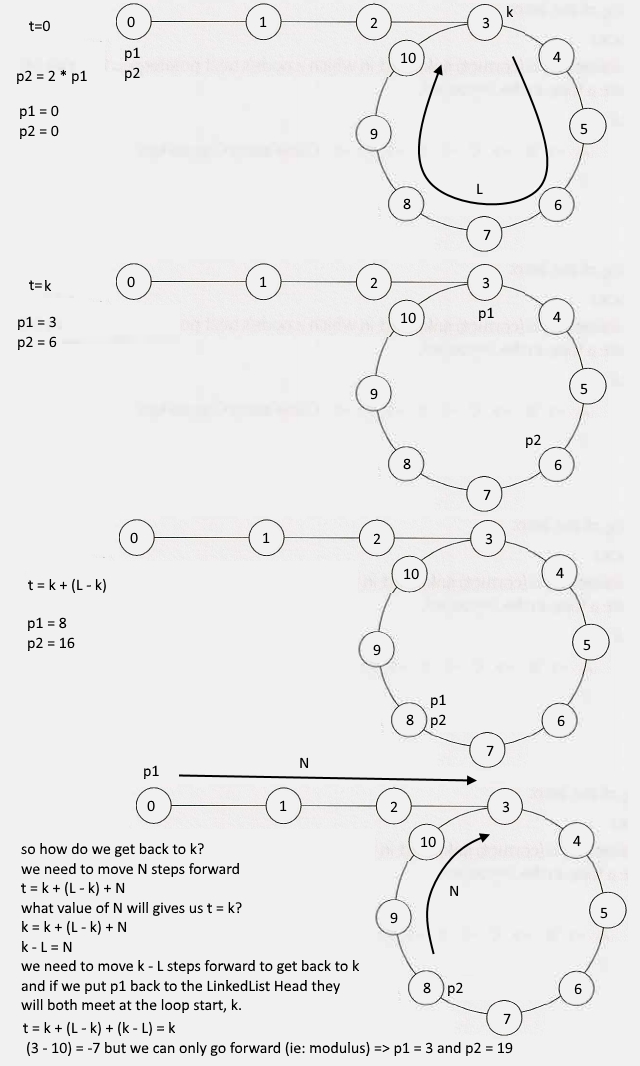
在时间t= k(3)时，p2距离头部(0)的距离是p1的两倍，因此要使它们回到直线上，我们需要p2‘追赶’到p1，还需要L- k(8) 5步才能完成。p2的速度是p1的2倍。

当t= k + (L ) (8)时，p2需要向前走k步才能回到k，如果我们将p1重新设置到头部(0)，我们知道如果p2以与p1相同的速度运行，p1和p2将分别以k(3，19 )的速度返回。

​

​

这是amit给出的解决方案。问题是，要么你知道，要么你不知道，但你无法在面试中弄清楚。因为我从来没有必要在链接列表中找到一个循环，除了通过面试之外，对我来说，知道它是没有意义的。所以对于面试官来说，把这说成面试问题，并期待amir的回答(这很好，因为它有线性的时间和零的额外空间)，这是相当愚蠢的。

因此，您的解决方案基本上是很好的，只是您应该使用哈希表，并且必须确保哈希表对节点的引用而不是对节点的引用。假设您有一个节点包含一个字符串和一个"next“指针，哈希函数会散列该字符串，并在字符串相等的情况下比较节点是否相等。在这种情况下，您会发现第一个节点具有重复的字符串，而不是循环开始时的节点，除非您非常小心。

(amir的解决方案在==比较对象而不是引用的语言中有一个非常类似的问题。例如，在Swift中，您必须使用=== (比较引用)，而不是== (比较对象)。