矩阵4x4中最后一行的魔术4用于3D图形的目的是什么?
当我读到关于WebGL的书时,我看到了下一个矩阵描述:
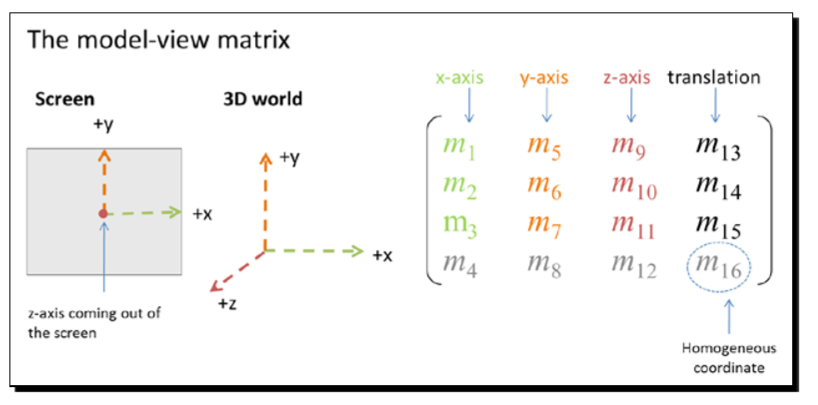
有关于书中最后一行的信息(WebGL初学者指南,Diego,Brandon ):
神秘的第四排,第四排,没有任何特殊的含义。元素m4,m8,m12总是零。元素m16(齐次坐标)总是1。
所以,如果最后一行总是[ 0, 0, 0, 1 ],我就不明白下一行是什么:
为什么必须严格地使用
[ 0, 0, 0, 1 ],为什么不只是所有的值都是0,甚至是其他值呢?
但是,如果要查看glMatrix javascript库的源代码,则完全是mat4 https://github.com/toji/gl-matrix/blob/master/src/gl-matrix/mat4.js中的translate()方法。
你可以看到下一个:
/**
* Translate a mat4 by the given vector not using SIMD
*
* @param {mat4} out the receiving matrix
* @param {mat4} a the matrix to translate
* @param {vec3} v vector to translate by
* @returns {mat4} out
*/
mat4.scalar.translate = function (out, a, v) {
var x = v[0], y = v[1], z = v[2],
a00, a01, a02, a03,
a10, a11, a12, a13,
a20, a21, a22, a23;
if (a === out) {
out[12] = a[0] * x + a[4] * y + a[8] * z + a[12];
out[13] = a[1] * x + a[5] * y + a[9] * z + a[13];
out[14] = a[2] * x + a[6] * y + a[10] * z + a[14];
out[15] = a[3] * x + a[7] * y + a[11] * z + a[15];
} else {
a00 = a[0]; a01 = a[1]; a02 = a[2]; a03 = a[3];
a10 = a[4]; a11 = a[5]; a12 = a[6]; a13 = a[7];
a20 = a[8]; a21 = a[9]; a22 = a[10]; a23 = a[11];
out[0] = a00; out[1] = a01; out[2] = a02; out[3] = a03;
out[4] = a10; out[5] = a11; out[6] = a12; out[7] = a13;
out[8] = a20; out[9] = a21; out[10] = a22; out[11] = a23;
out[12] = a00 * x + a10 * y + a20 * z + a[12];
out[13] = a01 * x + a11 * y + a21 * z + a[13];
out[14] = a02 * x + a12 * y + a22 * z + a[14];
out[15] = a03 * x + a13 * y + a23 * z + a[15];
}
return out;
};我会特别指出这句话:
out[15] = a03 * x + a13 * y + a23 * z + a[15];最后一个(齐次坐标)正在修改,所以它可能不等于1.0?
所以我不太明白..。
我知道,内部3x3矩阵代表旋转,[ m13, m14, m15 ]是改变相机原点位置的平移向量,但是最后一行是什么,为什么有时我会在库中看到一些计算呢?
PS
另外,我想对于3x3矩阵有某种magic 3,它用于2D-变换,对吗?
回答 1
Stack Overflow用户
发布于 2015-09-14 14:31:49
让我们从一些理论开始:
通常,OpenGL中的所有变换都是不同向量空间之间的映射。这意味着转换t从空间V中获取一个元素,并将其映射到空间W中的相应元素,该元素可以编写为
t: V ---> W最简单的映射之一是线性映射,它可以(在某些假设下**)总是由矩阵表示。矩阵的维数总是由我们正在工作的向量空间的维数确定,因此从R^N到R^M的映射总是这样:
t: R^N ---> R^M
t(x) = A * x, A = R^(N,M)其中A是N乘以M维矩阵。
在OpenGL中,我们通常需要从R^3到R^3的映射,这意味着线性映射总是用3x3矩阵表示。使用它,至少可以表示旋转、标度(以及这个*的组合)。但是,当查看(例如)翻译时,我们发现无法使用3x3矩阵来表示它们,因此我们必须扩展转换以支持这些操作。
这可以通过使用仿射映射来实现,而不是线性的,后者被定义为
t: R^N ---> R^M
t(x) = A * x + b, A = R^(N,M) is a linear transformation and b = R^M利用这一点,我们可以通过指定一个3x3矩阵和一个3D向量来表示从R^3到R^3的旋转、标度和变换。由于这个公式不是很方便(需要一个矩阵和一个向量,很难组合多个转换),所以通常将操作存储在维数N+1的矩阵中,这称为增广矩阵(或增广向量空间):
t: R^N ---> R^M
-A- b x
t(x) = [ ] * [ ]
-0- 1 1正如你所看到的,矩阵的最后一行总是零,除了最右边的元素。这也保证了结果t(x)的最后维数总是1。
为什么必须严格地使用
[ 0, 0, 0, 1 ],为什么不只是所有的值都是0,甚至是其他值呢?
如果我们不把最后一行严格限制为[0,0,0,1],那么R^3中就不再有增广仿射映射,而是R^4中的线性映射。因为在OpenGL中,R^4不是真正相关的,所以我们希望保留平移,最后一行是固定的。另一点是,当最后一行不同时,通过矩阵乘法组合仿射映射将不起作用。
剩下的一个问题是,我们仍然不能用仿射映射来表达(透视)投影。当查看OpenGL中的透视投影矩阵时,人们会注意到,这里的最后一行不是[0,0,0,1],但背后的理论完全不同(如果您感兴趣,请看这里或这里)。
最后一行是什么?为什么有时我在库中看到一些计算?最后一个(齐次坐标)正在修改,所以它可能不等于1.0?
如前所述,最后一行只是仿射映射的[0,0,0,1],而不是射影映射。但是有时在投影之后应用转换是有意义的(例如,在屏幕上移动投影图像),然后矩阵的最后一行必须得到尊重。这就是为什么大多数矩阵库以允许通用矩阵的方式实现所有操作的原因。线
out[15] = a03 * x + a13 * y + a23 * z + a[15];只要最后一行(a03、a13、a23、a15)等于[0,0,0,1],就会产生1。
既然这篇文章比我想象的要长得多,我最好在这里停下来,但是如果你还有其他问题,只要问一问,我就试着在答案中添加一些内容。
脚注:
**当两个空间都是有限维向量空间,并为它们定义一个基时,这两个空间都是有效的。
*组合,因为有限维空间上的线性变换组合也是线性的,例如t: R^N -> R^M,u: R^M -> R^K,都是线性=> t(u(x))线性的。
https://stackoverflow.com/questions/32565827
复制相似问题

