切分matlab的结果或精确的结果
切分matlab的结果或精确的结果
提问于 2015-09-24 02:55:14
我有一个关于在MATLAB中求解四次方程的问题,请参阅here。
MATLAB函数如下所示:
MATLAB
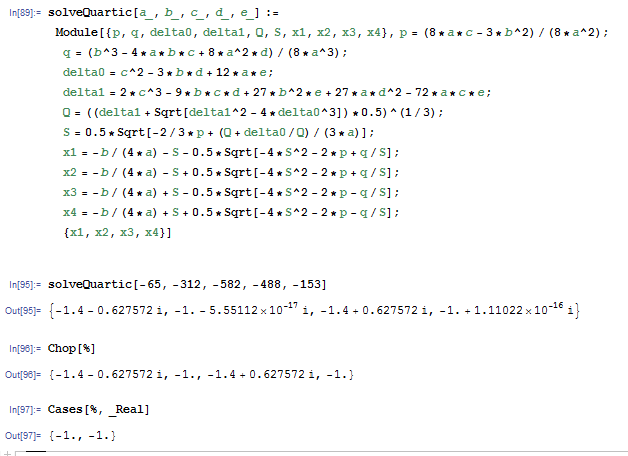
function [res] = solveQuartic(a, b, c, d, e)
p = (8*a*c - 3*b^2)/(8*a^2);
q = (b^3 - 4*a*b*c + 8*a^2*d)/(8*a^3);
delta0 = c^2-3*b*d + 12*a*e;
delta1 = 2*c^3 - 9*b*c*d + 27*b^2*e + 27*a*d^2 - 72*a*c*e;
Q = ((delta1 + sqrt(delta1^2 - 4*delta0^3))*0.5)^(1/3);
S = 0.5*sqrt(-2/3*p + (Q + delta0/Q)/(3*a));
x1 = -b/(4*a) - S - 0.5*sqrt(-4*S^2-2*p + q/S);
x2 = -b/(4*a) - S + 0.5*sqrt(-4*S^2-2*p + q/S);
x3 = -b/(4*a) + S - 0.5*sqrt(-4*S^2-2*p - q/S);
x4 = -b/(4*a) + S + 0.5*sqrt(-4*S^2-2*p - q/S);
res = [x1; x2; x3; x4];
end测试
solveQuartic(-65, -312, -582, -488, -153)
(*
-1.400000000000000 - 0.627571632442189i
-1.000000000000000 + 0.000000000000000i
-1.400000000000000 + 0.627571632442189i
-1.000000000000000 + 0.000000000000000i
*)

显然,四次方程$$-65x^4-312 x^3-582 x^2-488 x-153=0$拥有两个real roots。
现在,我要详细说明四次方程的real roots,我的试验如下
function [res] = solveQuarticReals(a, b, c, d, e)
p = (8*a*c - 3*b^2)/(8*a^2);
q = (b^3 - 4*a*b*c + 8*a^2*d)/(8*a^3);
delta0 = c^2-3*b*d + 12*a*e;
delta1 = 2*c^3 - 9*b*c*d + 27*b^2*e + 27*a*d^2 - 72*a*c*e;
Q = ((delta1 + sqrt(delta1^2 - 4*delta0^3))*0.5)^(1/3);
S = 0.5*sqrt(-2/3*p + (Q + delta0/Q)/(3*a));
x1 = -b/(4*a) - S - 0.5*sqrt(-4*S^2-2*p + q/S);
x2 = -b/(4*a) - S + 0.5*sqrt(-4*S^2-2*p + q/S);
x3 = -b/(4*a) + S - 0.5*sqrt(-4*S^2-2*p - q/S);
x4 = -b/(4*a) + S + 0.5*sqrt(-4*S^2-2*p - q/S);
res = [x1; x2; x3; x4];
%exact the real roots
j = 0;
for i = 1 : length(res)
if imag(res(i)) == 0
j = j + 1;
mid(j) = res(i);
end
end
res = mid;
end然而,它失败了。
发问
- 在MATLAB中真正的根有多精确?
- 或者在Mathematica中有一个内置的类似于
Chop的
回答 1
Stack Overflow用户
回答已采纳
发布于 2015-09-24 04:15:09
a=-65;
b=-312;
c=-582;
d=-488;
e=-153;
p = (8*a*c - 3*b^2)/(8*a^2);
q = (b^3 - 4*a*b*c + 8*a^2*d)/(8*a^3);
delta0 = c^2-3*b*d + 12*a*e;
delta1 = 2*c^3 - 9*b*c*d + 27*b^2*e + 27*a*d^2 - 72*a*c*e;
Q = ((delta1 + sqrt(delta1^2 - 4*delta0^3))*0.5)^(1/3);
S = 0.5*sqrt(-2/3*p + (Q + delta0/Q)/(3*a));
x1 = -b/(4*a) - S - 0.5*sqrt(-4*S^2-2*p + q/S);
x2 = -b/(4*a) - S + 0.5*sqrt(-4*S^2-2*p + q/S);
x3 = -b/(4*a) + S - 0.5*sqrt(-4*S^2-2*p - q/S);
x4 = -b/(4*a) + S + 0.5*sqrt(-4*S^2-2*p - q/S);
res = [x1; x2; x3; x4];
%exact the real roots
realNumber = real(res((abs(imag(res)) <= 1e-10)))请试试这些密码。由于浮点数据类型的特点,即使两个数值在数学上是相同的,imag(S)和imag(0.5*sqrt(-4*S^2-2*p + q/S))之间也会有一些差别。为了检查错误,请在matlab窗口中键入"format shortEng“,然后键入imag(S) - imag(0.5*sqrt(-4*S^2-2*p + q/S))。答案是55.5112e-018i。答案的图像数肯定不是0,而是55.5112e-018。这一现象是由浮点数据类型的性质造成的。
PS。非常感谢Stewie Griffin!
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/32752569
复制相关文章
相似问题

