Python中的加速MSD计算
Python中的加速MSD计算
提问于 2015-10-07 09:12:04
这是对社区的一个呼吁,看看是否有人想要提高这个MSD计算实现的速度。它很大程度上是基于以下博客文章的实现:http://damcb.com/mean-square-disp.html
目前,对于5000点的二维轨迹,目前的实现大约需要9s。如果你需要计算很多轨迹的话.
我没有尝试将其并行化(使用multiprocess或joblib),但我觉得创建新进程对于这种算法来说太重了。
以下是代码:
import os
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# Parameters
N = 5000
max_time = 100
dt = max_time / N
# Generate 2D brownian motion
t = np.linspace(0, max_time, N)
xy = np.cumsum(np.random.choice([-1, 0, 1], size=(N, 2)), axis=0)
traj = pd.DataFrame({'t': t, 'x': xy[:,0], 'y': xy[:,1]})
print(traj.head())
# Draw motion
ax = traj.plot(x='x', y='y', alpha=0.6, legend=False)
# Set limits
ax.set_xlim(traj['x'].min(), traj['x'].max())
ax.set_ylim(traj['y'].min(), traj['y'].max())以及产出:
t x y
0 0.000000 -1 -1
1 0.020004 -1 0
2 0.040008 -1 -1
3 0.060012 -2 -2
4 0.080016 -2 -2

def compute_msd(trajectory, t_step, coords=['x', 'y']):
tau = trajectory['t'].copy()
shifts = np.floor(tau / t_step).astype(np.int)
msds = np.zeros(shifts.size)
msds_std = np.zeros(shifts.size)
for i, shift in enumerate(shifts):
diffs = trajectory[coords] - trajectory[coords].shift(-shift)
sqdist = np.square(diffs).sum(axis=1)
msds[i] = sqdist.mean()
msds_std[i] = sqdist.std()
msds = pd.DataFrame({'msds': msds, 'tau': tau, 'msds_std': msds_std})
return msds
# Compute MSD
msd = compute_msd(traj, t_step=dt, coords=['x', 'y'])
print(msd.head())
# Plot MSD
ax = msd.plot(x="tau", y="msds", logx=True, logy=True, legend=False)
ax.fill_between(msd['tau'], msd['msds'] - msd['msds_std'], msd['msds'] + msd['msds_std'], alpha=0.2)以及产出:
msds msds_std tau
0 0.000000 0.000000 0.000000
1 1.316463 0.668169 0.020004
2 2.607243 2.078604 0.040008
3 3.891935 3.368651 0.060012
4 5.200761 4.685497 0.080016
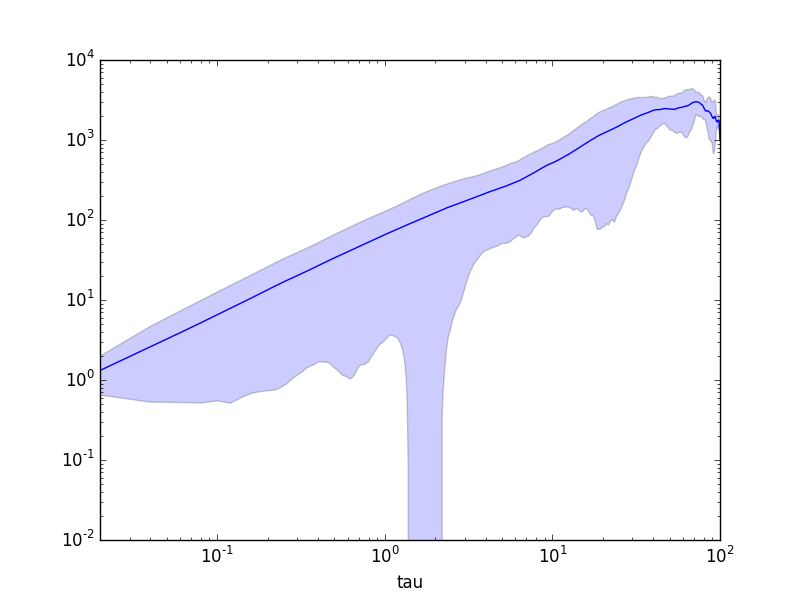
还有一些简介:
%timeit msd = compute_msd(traj, t_step=dt, coords=['x', 'y'])给这个:
1 loops, best of 3: 8.53 s per loop知道吗?
回答 5
Stack Overflow用户
回答已采纳
发布于 2015-12-11 14:10:11
到目前为止所提到的MSD计算都是O(N**2),其中N是时间步长的数目。使用FFT,这可以简化为O(N*log(N))。有关python的解释和实现,请参见this question and answer。
编辑:一个小的基准(我还添加了这个基准测试to this answer):用
r = np.cumsum(np.random.choice([-1., 0., 1.], size=(N, 3)), axis=0)对于N=100.000,我们得到
$ %timeit msd_straight_forward(r)
1 loops, best of 3: 2min 1s per loop
$ %timeit msd_fft(r)
10 loops, best of 3: 253 ms per loopStack Overflow用户
发布于 2015-10-07 11:36:42
它一条一条地做了一些分析,看起来熊猫正在慢慢地做这件事。这个纯粹的numpy版本大约快14倍:
def compute_msd_np(xy, t, t_step):
shifts = np.floor(t / t_step).astype(np.int)
msds = np.zeros(shifts.size)
msds_std = np.zeros(shifts.size)
for i, shift in enumerate(shifts):
diffs = xy[:-shift if shift else None] - xy[shift:]
sqdist = np.square(diffs).sum(axis=1)
msds[i] = sqdist.mean()
msds_std[i] = sqdist.std(ddof=1)
msds = pd.DataFrame({'msds': msds, 'tau': t, 'msds_std': msds_std})
return msdsStack Overflow用户
发布于 2015-10-07 13:49:58
以上补充了moarningsun的答案:
- 您可以加快使用numexpr
- 如果您以日志比例尺绘制MSD,则不需要每次计算 将numpy作为np导入numexpr def logSpaced(L,pointsPerDecade=15):“”生成一个小于L“numpy= np.log10(L)返回np.unique(np.logspace( start=0,stop=nbdecades,num=nbdecades * pointsPerDecade,base=10,endpoint=False ).astype(int)) def compute_msd(xy,pointsPerDecade=15):dts =logSpaced(Xy),( pointsPerDecade) (Dts):sqdist = numexpr.evaluate( '(a-b)**2',{'a':xy:- dt,'b':xydt:} ).sum(axis=-1) msdi = sqdist.mean() msd_stdi = sqdist.std(ddof=1) msds = pd.DataFrame({' msds ':msd,‘τ’:dt,'msds_std':msd_std})返回msd。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/32988269
复制相关文章
相似问题

