顶点数最大的最短路径
我想找到两个顶点之间的最短路径,并附加一个约束:可以访问最大n个顶点。图是有向的、连通的、非负的权值,并且可能包含圈。
示例:
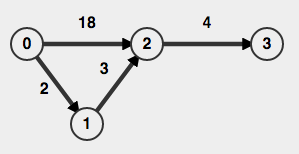
- 最短路径0->2,n = 2是18
- 最短路径0->3,n = 3是22
- 最短路径0->3,n = 4是9
到目前为止,我已经实现了得到简单最短路径的贾克斯特拉斯算法,我的想法是保持当前访问顶点的计数器,如果它超过n,它需要后退一步或多步,然后尝试另一条路径。但据我所知,正如这里所解释的那样,贾克斯特拉斯不能用于回溯。
另一个想法是以某种方式存储表中每个节点之间的每条路径。但是我不太清楚贾克斯特拉怎么能发现重量为18的路径0->2,因为它并不是一条最短的路径.
有没有人知道如何解决这个问题?
回答 4
Stack Overflow用户
发布于 2015-10-27 04:12:29
将每个顶点划分为n顶点,即对于顶点u,我们创建表示为(u, 1) ... (u, n)的n顶点,第二个数表示到该顶点的步骤数。对于u到v的每一条边,我们在新图中创建了一个从(u,i)到(v,i+1)的边,其中1<=i<=n-1。现在,如果您想用n计算u与v之间的最短路径,只需从(u,1)处执行Dijkstra,则您的答案是min(result (v, i) | 1<=i<=n)。
顶点的总数可以是n*n,所以复杂度是关于O(n^2*log(n^2))的。
Stack Overflow用户
发布于 2015-10-27 04:38:14
设COST_TO(v,n)是顶点v与n条边的最小路径的总权重。
当n=0时,答案很简单:
对于所有v,如果v是源顶点,则COST_T(v,0) =0,否则为无穷大。
对于n>0,COST_TO(v,n)是COST_TO(v,n-1)和所有COST_TO(w,n-1)+权重(w,v)的最小值,其中有从w到v的边。
因此,对于n=0到N,跟踪COST_(v,n) <无穷大的所有顶点及其代价,并根据n-1的值计算n的代价。
同时,您可以跟踪每个v的最小权重路径--每次使用边规则将成本更新为v时,v的新路径就是w+那个边的路径。一个反向单一链接的列表是方便的。
Stack Overflow用户
发布于 2015-10-27 04:16:16
https://stackoverflow.com/questions/33359731
复制相似问题

