傅里叶拟合系数
傅里叶拟合系数
提问于 2015-11-01 00:11:59
最近,我正在将傅里叶级数函数拟合成周期信号,以便通过最小二乘法检索每个分量的幅值和相位,因此我修改了这文件的代码:
import math
import numpy as np
#period of the signal
per=1.0
w = 2.0*np.pi/per
#number of fourier components.
nf = 5
fp = open("file.cat","r")
# m1 is the number of unknown coefficients.
m1 = 2*nf + 1
# Create empty matrices.
x = np.zeros((m1,m1))
y = np.zeros((m1,1))
xi = [0.0]*m1
# Read (time, value) from each line of the file.
for line in fp:
t = float(line.split()[0])
yi = float(line.split()[1])
xi[0] = 1.0
for k in range(1,nf+1):
xi[2*k-1] = np.sin(k*w*t)
xi[2*k] = np.cos(k*w*t)
for j in range(m1):
for k in range(m1):
x[j,k] += xi[j]*xi[k]
y[j] += yi*xi[j]
fp.close()
# Copy to big matrices.
X = np.mat( x.copy() )
Y = np.mat( y.copy() )
# Invert X and multiply by Y to get coefficients.
A = X.I*Y
A0 = A[0]
# Solution is A0 + Sum[ Amp*sin(k*wt + phi) ]
print "a[0] = %f" % A[0]
for k in range(1,nf+1):
amp = math.sqrt(A[2*k-1]**2 + A[2*k]**2)
phs = math.atan2(A[2*k],A[2*k-1])
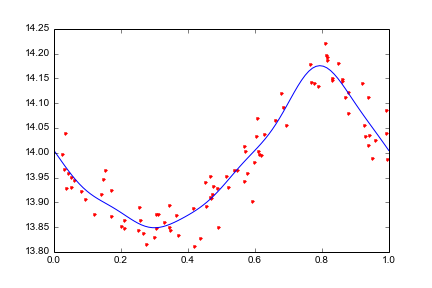
print "amp[%d] = %f phi = %f" % (k, amp, phs)但情节显示了这一点(当然没有要点):

它应该展示出这样的东西:
有人可以告诉我如何用另一种更简单的方法来计算相位和振幅?也许是个导游,我会非常感激的。干杯!
警局。我将附加我使用的文件,仅仅是因为:)
编辑
错误的索引是:(
首先,我用以下值定义了向量:
amp = np.array([np.sqrt((A[2*k-1])**2 + (A[2*k])**2) for k in range(1,nf+1)])
phs = np.array([math.atan2(A[2*k],A[2*k-1]) for k in range(1,nf+1)])然后,为了建立信号,我定义了:
def term(t): return np.array([amp[k]*np.sin(k*w*t + phs[k]) for k in range(len(amp))])
Signal = np.array([A0+sum(term(phase[i])) for i in range(len(mag))])但是在np.sin()中,k应该是k+1,因为索引从0·__·开始
def term(t): return np.array([amp[k]*np.sin((k+1)*w*t + phs[k]) for k in range(len(amp))])
plt.plot(phase,Signal,'r-',lw=3)
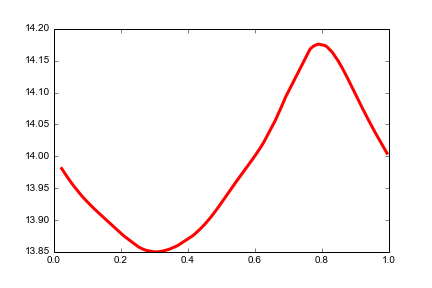
仅此而已。
谢谢马可·汤皮塔克的帮助!
回答 1
Stack Overflow用户
回答已采纳
发布于 2015-11-01 00:52:40
您为信号指定了错误的时间段:
#period of the signal
per=0.178556这给出了最终的傅里叶拟合,实际上,最大周期是0.17。问题是,这个数字指定了傅立叶级数中存在的最长周期。该函数只有0.17或更短的部分。很明显,你是在期待一个周期~1的契合,所以它永远无法恰当地近似。您应该指定per=1.0。该算法没有什么问题;快速编写类似的算法给出了同样的输出和可信的结果:

页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/33457955
复制相关文章
相似问题

