曲线直线的直线识别算法
我不熟悉我将要在这里描述的问题。很抱歉用错了术语。
我要找的是一个算法(最好是C/C++中的库)来识别曲线上的直线部分。输入曲线使用一组(x,y)形式的有序点来定义。我发现了一些关于Hough变换和一个libray OpenCV的文章。使用OpenCV似乎是可能的,但看起来有点过火。我需要一个非常有效的算法来处理一条简单的曲线。有什么办法吗?谢谢。
更新:参见下面的示例,目标是识别红色部分
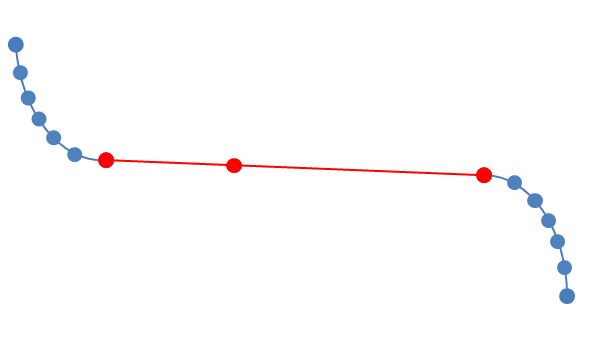
正如一些人指出的那样,直线部分可能不一定是直线的,也就是说,在这里我可能需要一些偏差的容忍。
回答 3
Stack Overflow用户
发布于 2016-01-04 12:17:08
计算连续点O(N)之间的斜率。
如果三个连续点在两对之间的斜率几乎相同,那么这三个点几乎处于同一条线上(减去舍入误差)。因此,要找到直线,只需寻找斜坡几乎相等的连续点的部分。你可以在一次通过点O(N)来做这件事。
如果你有很多点,你可以遇到这样的情况:曲线很小,比你在比较斜率时允许的四舍五入误差小。如果您看到这一点,添加另一个检查,以比较第一个斜率在直线上,以确保您不会复合错误。
如果您需要更全面或更快的东西,请考虑使用OpenCV。
Stack Overflow用户
发布于 2016-01-04 13:14:14
假设你连续3个积分-- (x1,y1),(x2,y2)和(x3,y3)
计算(y1-y2)*(x3-x2) + (x2-x1)*(y3-y2)
如果这是正的,那么这条曲线在(x2,y2)向左转,如果它是负的,那么它就向右转。如果为零,则曲线在(x2,y2)处是直线的。
要找到真正的直线部分,你可以寻找点,这是零。你可能真的很想找到它从左转到右转的地方。
如果你想要一个实际的衡量它转动的多少,那么除以length(segment1)*length(segment2),结果就是转角的罪恶。
Stack Overflow用户
发布于 2016-01-04 13:03:00
我不知道为什么那些日子我和RANSAC有着无尽的爱。我甚至在做饭的时候试着用它。但是,RANSAC和fit-line模型可能是解决问题的最佳解决方案。因为你有很多的离群点(非直线点)和你有一个好的不稳定性(直线点)。在这里,您可以在C++中找到一个现成的实现。RANSAC-like implementation for arbitrary 2D sets
https://stackoverflow.com/questions/34590169
复制相似问题

