从二维网格生成多边形的有效算法?(vertices+edges)
从二维网格生成多边形的有效算法?(vertices+edges)
提问于 2016-02-17 22:13:46
给定一个由顶点(2D坐标)和边(作为顶点对)组成的网格,如下所示:
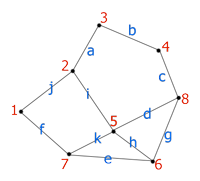
因此,边的定义如下:
a: 2,3
b: 3,4
c: 4,8
d: 5,8
e: 6,7
etc..边是方向中立的,即定义边的任意两个顶点的顺序是随机的(边不是顺时针或逆时针方向)。
多边形可能是凸的,也可能是凹的,但它们从不重叠或自相交(边永远不会相交)。
问题:如何生成所有多边形的列表?
更具体地说,在上面的例子中,我需要4个多边形,如下所示:
(a,b,c,d,i)
(d,g,h)
(f,i,j,k)
(e,h,k)多边形也没有方向,顺时针方向或逆时针方向不适用,事实上,定义多边形的边的顺序也可能是随机的。例如,(a,i,d,b,c) 5边的也可以.
与其将多边形定义为边列表,它还可以是连通顶点的列表,如下所示:
(2,3,4,8,5)
(6,5,8)
(2,5,7,1)
(7,6,5)在这种情况下,顶点的顺序不能是随机的(顶点列表应该是一个圆形序列),但是方向(顺时针方向或逆时针方向)仍然是不相关的。因此,四边多边形也可以是(5,2,1,7)或(1,7,5,2)等。
什么是有效的(快速)方法来构造一个多边形列表,定义在边或顶点?
回答 1
Stack Overflow用户
发布于 2016-02-17 22:45:47
对于每个边vw,生成两个半边v->w和w->v。通过头( x->y的头是y)来划分它们。在每个分区中,按角度排序(如果使用比较排序,那么有一种方法可以避免trig)。
对于示例图,结果是
7->1, 2->1
1->2, 5->2, 3->2
2->3, 4->3
8->4, 3->4
7->5, 6->5, 8->5, 2->5
8->6, 5->6, 7->6
6->7, 5->7, 1->7
5->8, 6->8, 4->8。现在,定义一个置换,其中v->w映射到包含w->v的列表中的w->v后面的半边(如果必要的话)。这个排列的循环是多边形。
例如,5->8映射到2->5 (在8->5之后)映射到3->2 (5->2后)映射到4->3 (在2->3之后)映射到8->4 (在3->4之后)映射到5->8 (在4->8之后)。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/35468830
复制相关文章
相似问题

