Taylor级数-计算sin(x)直到6位精度
Taylor级数-计算sin(x)直到6位精度
提问于 2016-02-22 17:54:08
我必须用Taylor级数计算sin(x),直到输出有6位小数点。这个论点是一个角度。我没有实现检查小数位,我只是打印下一个值(检查它是否有效),但是经过10-20的迭代,它显示了无穷大/NaN的值。
我的想法怎么了?
public static void sin(double x){
double sin = 0;
int n=1;
while(1<2){
sin += (Math.pow(-1,n) / factorial(2*n+1)) * Math.pow(x, 2*n+1);
n++;
try {
Thread.sleep(50);
} catch (InterruptedException ex) {
}
// CHECKING THE PRECISION HERE LATER
System.out.println(sin);
}
}方程式:
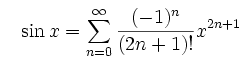
回答 3
Stack Overflow用户
回答已采纳
发布于 2016-02-22 18:34:33
不要用阶乘和幂来计算每一项!你很快就会溢出。只需意识到下一项是-term *x*x/ ((n+1)*(n+2)),其中n对每项增加2:
double tolerance = 0.0000007; // or whatever limit you want
double sin = 0.;
int n = 1;
double term = x;
while ( Math.abs(term) > tolerance ) {
sin += term;
term *= -( (x/(n+1)) * (x/(n+2)) );
n+= 2;
}Stack Overflow用户
发布于 2016-02-22 18:37:11
要添加到@Xoce (和@FredK)提供的答案,请记住您正在计算McLaurin系列(泰勒关于x = 0的特例)。虽然对于大约pi/2为零的值,这将很快收敛,但在阶乘对x值进行进一步分解之前,您可能无法得到数字的收敛。
我的建议是使用关于sin(x)最接近值的实际泰勒级数,它的确切值是已知的(即,pi/2的最近倍数,而不仅仅是零)。一定要做好会聚检查!
Stack Overflow用户
发布于 2016-02-22 17:58:25
问题:
NAN错误通常是一个很大的数字,如果除以2个数字,但除数很小,或者是零,就会发生这种情况。
解决方案
之所以会发生这种情况,是因为您的阶乘数正在溢出,并且在以后的某个点上,如果您的阶乘被作为参数(一个int ),那么您将再次将其除以零,然后将其更改为,例如,一个BIgInterger对象。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/35560530
复制相关文章
相似问题

