R^n中立方体/球面上的网格搜索
我正试图在R^n中的一个领域( n是未知的)上实现网格搜索(如果这很重要的话)。
输入包括球体的半径和中心,以及控制网格分辨率的超参数theta。我想用这三个参数的函数来表达这一领域中的每一点。
我也愿意考虑立方体搜索,只迭代立方体的面。(即,迭代球体
如果我知道n=2,我会做的是:
import numpy as np
def enumerate_2d_sphere(R,theta,center=(0,0)):
for n in xrange(int(2*np.pi / theta)+1):
degree = n*theta
point =(center[0]+R*np.cos(degree),center[1]+R*np.sin(degree))
yield point
for p in enumerate_2d_sphere(1,0.1):
print p由于n可以任意大,所以我正在寻找一种高效地迭代球面\多维数据集的方法。
有什么想法吗?
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
最后,我使用了一种修改版本,用的是可靠的建议:
import itertools
import numpy as np
import matplotlib.pyplot as plt
def f(d, center, scale=1):
dim = len(center)
print d/-2.0
diff = scale * np.array([d/-2.0 for _ in xrange(dim)])
bias = diff + center
for i in range(dim):
l = ([ xrange(1,d) for _ in xrange(i)] +
[[0,d]] +
[ xrange(d+1) for _ in xrange(dim-i-1)]
)
for r in itertools.product(*l):
yield scale*np.array(r)+bias
#example for R^2:
center = (1,1.5)
data = np.array([x for x in f(20,center,scale = 0.1)])
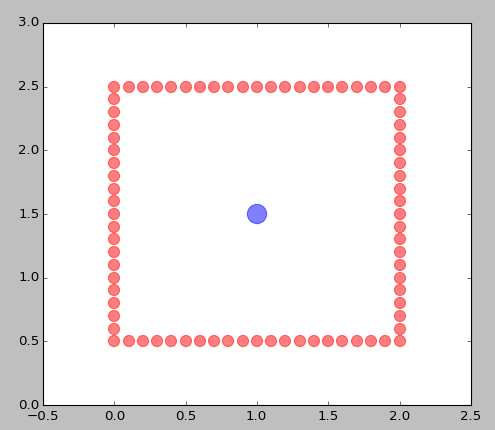
plt.scatter(data[:,0], data[:,1],color='r',s=100,alpha=0.5)
plt.scatter(center[0], center[1],color='b',s=300,alpha=0.5)
plt.show()产出数字:
另一种选择是生成球上均匀分布的样本。注意,样本数控制着点的“密度”(或预期密度):
import numpy as np
def generate_random_points(R,center,quantity=1000):
"""
:param R: float
:param center: np.array
:param quantity: int
"""
dim = len(center)
for n in xrange(quantity):
s = np.random.normal(0, 1,dim)
r = np.sqrt(np.dot(s,s))
s = (R/r) * s
yield s+center最糟糕的方法(就简单性和效率而言)是使用n-1角的计数在球面上生成点。缺乏效率的原因是需要经常计算产品sin和cos (尽管这也可能被黑客攻击)。
Stack Overflow用户
发布于 2016-02-28 08:52:19
您可以在n维中使用球面坐标(参见维基百科),也可以使用欧几里德坐标,只需将最后一个坐标设置为获得正确半径(正负)所需的任何位置。这两种方法都是很好的参数化,并且会给出球面上的所有点--有合适的参数数来迭代。
但是,它们不会自然地导致一个恒定的面积(体积)元素,这是很容易看到的,只要考虑到三个球。这个问题没有容易的解决办法。
我认为一种可能的方法是使用n-1维网格参数化,但是根据体积将第n个组件细分为一个可变的值数。
N个立方体的面更容易:只要生成n对面,其中n个坐标是极小的或最大的。例如,考虑从原点开始的大小为1的n个立方体:
将第一个坐标设置为零,并枚举剩余部分上的网格。然后把它设置为一个,然后再做一次。然后对第二个坐标重复。诸若此类。
这里有一个使用itertools.product的简单方法。为了简单和高效,我已经将这个框缩放成整数坐标:您需要重新排列并移动中心。因此,n是维数,d是每个轴上的细分数。
import itertools
def f(n,d):
for i in range(n):
l = ([ range(1,d-1) for _ in range(i)] +
[[0,d-1]] +
[ range(d) for _ in range(n-i-1)]
)
for r in itertools.product(*l):
yield r
print(list(f(4,3)))https://stackoverflow.com/questions/35680084
复制相似问题

