用欧拉法求解四维耦合系统
我想实现下面代码中给出的系统,但是当我将它增加到1500次迭代时,我会得到以下错误:
警告(来自警告模块):文件"D:\python测试文件\sys1.py“,第16行dy =c* x*z +w RuntimeWarning:在double_scalars警告中遇到溢出(来自警告模块):文件"D:\python测试文件\sys1.py”,第17行dz = -b*z + x*y RuntimeWarning: double_scalars警告中遇到的溢出(来自警告模块):文件"D:\python测试文件\sys1.py“,第18行du = -h*u - x*z RuntimeWarning: double_scalars警告中遇到的溢出(来自警告模块):文件"D:\python测试文件\sys1.py“,第42行zsi+1 = zsi + (dz * t) RuntimeWarning: double_scalars警告中遇到的无效值(来自警告模块):文件"D:\python测试文件\sys1.py”,第15行dx = a*(y-x) +u RuntimeWarning:在double_scalars警告中遇到的无效值(来自警告模块):文件"D:\python测试文件\sys1.py“,第19行dw = k1*x - k2*y RuntimeWarning:在double_scalars警告中遇到的无效值(来自警告模块):文件RuntimeWarning第156行txs,tys,tzs = vecw/w,vecw 1/w,vecw 2/w RuntimeWarning:在除法中遇到的无效值
我的代码:
from __future__ import division
import numpy as np
import math
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# import pdb
# pdb.set_trace()
def sys1(x, y, z, u, w , a=10, b=8.0/3.0, c=28, k1=0.4, k2=8, h=-2):
dx = a*(y-x) + u
dy = c*x- x*z + w
dz = -b*z + x*y
du = -h*u - x*z
dw = k1*x - k2*y
return dx, dy, dz, du, dw
t = 0.01
itera = 2500
# Need one more for the initial values
xs = np.empty((itera+1,))
ys = np.empty((itera+1,))
zs = np.empty((itera+1,))
us = np.empty((itera+1,))
ws = np.empty((itera+1,))
# Setting initial values
xs[0], ys[0], zs[0], us[0], ws[0] = (0.1, 0.1, 0.1, 0.1, 0.1)
# Stepping through "time".
for i in range(itera):
# Derivatives of the X, Y, Z state
dx, dy, dz, du, dw = sys1(xs[i], ys[i], zs[i], us[i], ws[i])
xs[i+1] = xs[i] + (dx * t)
ys[i+1] = ys[i] + (dy * t)
zs[i+1] = zs[i] + (dz * t)
us[i+1] = us[i] + (du * t)
ws[i+1] = ws[i] + (dw * t)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(xs, ys, zs)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")
plt.show()回答 1
Stack Overflow用户
发布于 2016-03-27 01:05:20
你正试图用一个著名的简单的数值格式来模拟一个著名的非线性微分方程组(实际上是以敏感著称的系统的一个缓冲版本)。您的解决方案在给定的时间步骤中出现分叉,这表现在您的解决方案值首先成为inf (您没有注意到),然后是nan (您仍然没有注意到),然后Axes3D.plot中的缩放产生了一个零的除法,同时在您的无穷大范围内杂耍。
以下是您的输出:
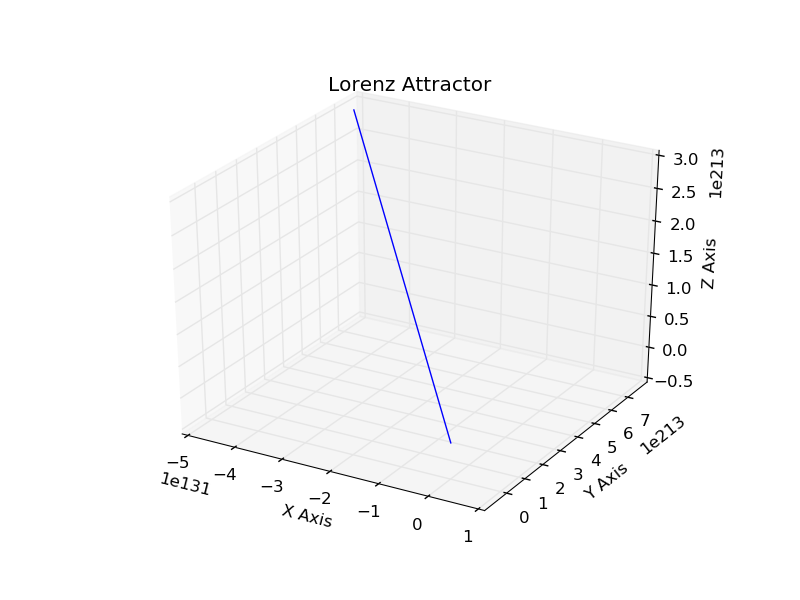
注意轴的极限刻度:所有的都在1e100以上。这可能会告诉你你有无穷远的东西在到处跑。
好消息是,相同的程序可以通过减少时间步长来给出合理的输出,这应该是你第一次使用欧拉法(特别是从MATLAB实现中确信你的算法是正确的)。
使用t=0.001; itera=25000 (左)和t=0.0001; itera=250000 (右)的示例输出:
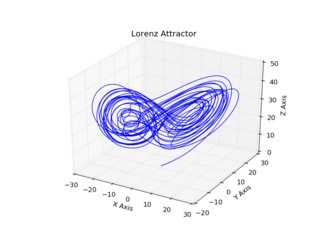
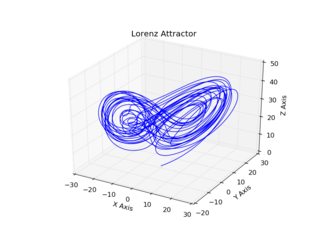
首先,请注意,这两个情节是相当合理的,公然有限。其次,请注意,这两种轨迹,虽然有一个大体相似的形状,是非常不同的。如果使用更长的迭代(我指的是较长的总t*itera),差异将逐渐变得更加发音,最终两个轨迹将完全分开。
您应该确保您明白,您正在使用非常不准确的方法来绘制一个非常敏感(准确地说是:混沌)系统的轨迹。即使使用非常精确的方法,您最终也会积累一些错误,并且会偏离初始值问题的实际解决方案。你所能希望的就是画出吸引子的粗糙形状,围绕它的轨迹必然是曲折的。但我很肯定这就是你的目标。
https://stackoverflow.com/questions/36151796
复制相似问题

