点到椭圆弧最短距离的算法
点到椭圆弧最短距离的算法
提问于 2016-03-28 10:51:24
我试图找到一种计算任意点与弧之间最短距离的通用方法,其中,圆弧是椭圆边界的90度部分,椭圆的轴与笛卡尔轴对齐。我的工作是2D,所以点和椭圆都是共面的。如果点与弧在同一象限内,相对于椭圆的中心,那么我认为这个问题与计算从一个点到整个椭圆边界上任何地方的距离是一样的,对此有相当简单的方法(例如http://www.geometrictools.com/Documentation/DistancePointEllipseEllipsoid.pdf)。
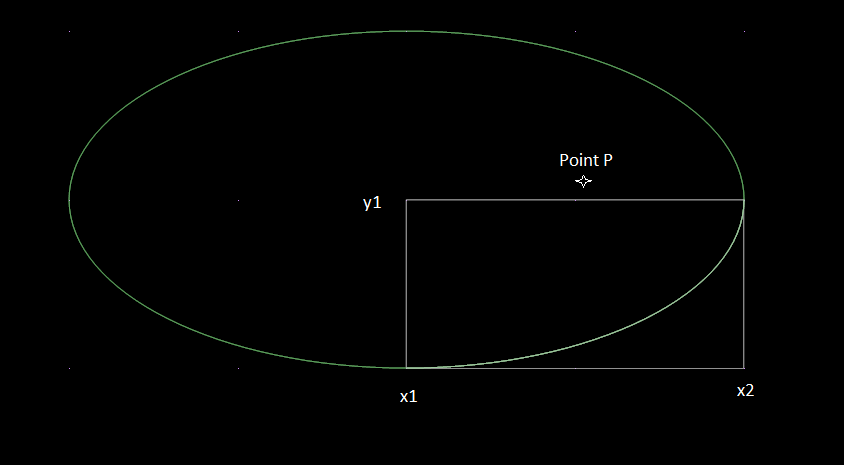
在图中,如果点在x1的左边、x2的右边或y1以下,那么问题就直接发生了。
但是,如果P点如图中所示,我想不出该做什么。
回答 2
Stack Overflow用户
发布于 2016-03-29 07:59:36
我通常使用这个椭圆:
- 用
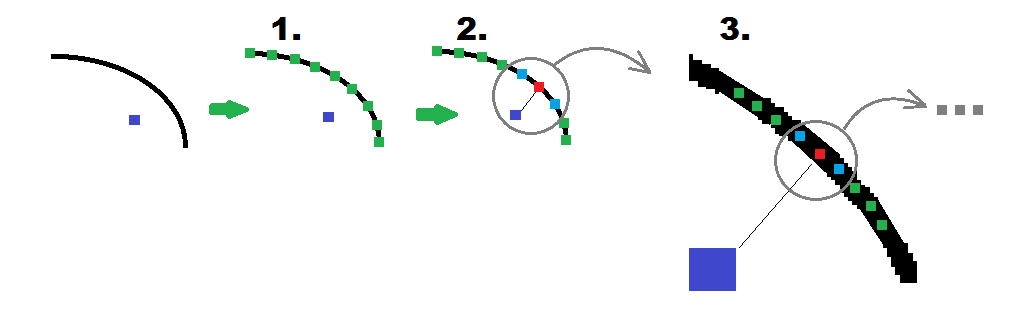
Npoints对电弧进行采样 对于90学位块,请使用N>=8,这样yu就不会错过一些东西 - 找到最近的点
- 由
Npoint 围绕该点进行的示例弧 从前一点到下一点的覆盖范围 - 递归循环到#2 每一次迭代/递归都提高了精度。如果达到所需的精度范围(采样区域足够小)或可变精度限制(以避免FPU的下溢),则停止。
Notes
这适用于任何椭圆弧,而不仅仅是轴对齐。
Edit1 C++示例
double x0,y0,rx,ry,a0,a1; // elliptic arc center,semi-axises,start/end angles CW
void ellarc_closest_point(double &x_out,double &y_out,double x_in,double y_in)
{
int e,i;
double ll,l,aa,a,da,x,y,b0,b1;
while (a0>=a1) a0-=pi2; // just make sure a0<a1
b0=a0; b1=a1; da=(b1-b0)/25.0; // 25 sample points in first iteration
ll=-1; aa=a0; // no best solution yet
for (i=0;i<3;i++) // recursions more means more accurate result
{
// sample arc a=<b0,b1> with step da
for (e=1,a=b0;e;a+=da)
{
if (a>=b1) { a=b1; e=0; }
// elliptic arc sampled point
x=x0+rx*cos(a);
y=y0-ry*sin(a); // mine y axis is in reverse order therefore -
// distance^2 to x_in,y_in
x-=x_in; x*=x;
y-=y_in; y*=y; l=x+y;
// remember best solution
if ((ll<0.0)||(ll>l)) { aa=a; ll=l; }
}
// use just area near found solution aa
b0=aa-da; if (b0<a0) b0=a0;
b1=aa+da; if (b1>a1) b1=a1;
// 10 points per area stop if too small area already
da=0.1*(b1-b0); if (da<1e-6) break;
}
x_out=x0+rx*cos(aa);
y_out=y0-ry*sin(aa); // mine y axis is in reverse order therefore -
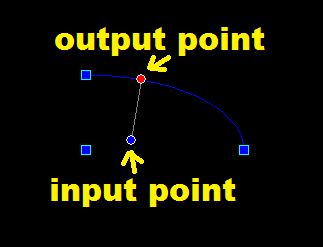
}和视觉输出:
Stack Overflow用户
发布于 2016-03-29 11:07:48
所以整个弧形都是一条红鲱鱼。这是一个线性比例回到一个单位圆。所以你只需要找到从一个点到单位圆的最短距离。(https://math.stackexchange.com/questions/103453/closest-point-to-a-unit-circle-from-a-point-inside-it)然后只需撤销比例和测量距离。
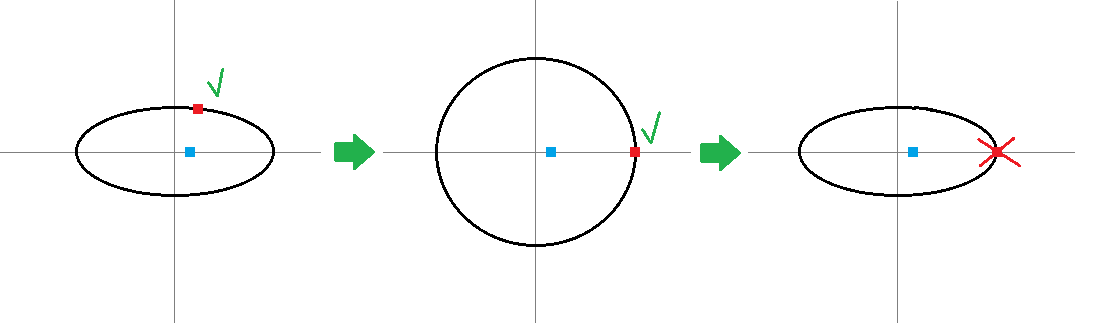
编辑这显然是错误的!
如果你找到最接近圆的点(在缩放空间中),那并不意味着这一点在重新标度后(到椭圆空间)仍然是最接近的!见示例:
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/36260793
复制相关文章
相似问题

