橙主成分分析与科学研究的不同结果-学习主成分分析
橙主成分分析与科学研究的不同结果-学习主成分分析
提问于 2016-04-04 11:24:29
我使用学习PCA来查找具有大约20000个特性和400+样本的数据集的主组件。
然而,与应该使用Orange3主成分分析的学习PCA相比,我得到了不同的结果.我也没有检查Orange3 PCA提出的规范化选项。
其中第一主成分占总方差的14%,第二主成分占13%等。
对于Orange3,我得到了一个非常不同的结果(第一个主成分的方差~65%,等等):
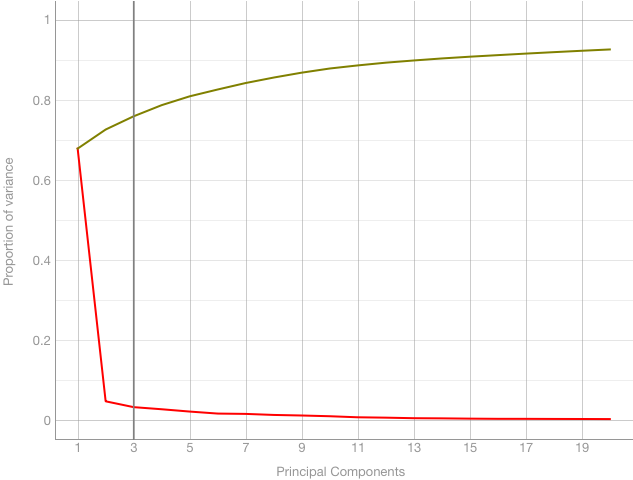
使用scikit-learn的代码如下所示:
import pandas as pd
from sklearn.decomposition import PCA
matrix = pd.read_table("matrix.csv", sep='\t', index_col=0)
sk_pca = PCA(n_components=None)
result = sk_pca.fit(matrix.T.values)
print(result.explained_variance_ratio_)使用Orange3,我使用文件块加载csv。然后,我将这个块连接到PCA块,在该块中,我不检查规范化选项。
这两种方法的区别是什么?
回答 3
Stack Overflow用户
回答已采纳
发布于 2016-04-06 10:24:44
由于K3--rnc的回答,我检查了我是如何加载数据的。
但是数据被正确加载,没有丢失数据。问题是,Orange3加载数据--将特性放在列上,样本放在行上,这与我所期望的相反。
因此,我转换了数据,结果与scikit-learn模块给出的结果相同:
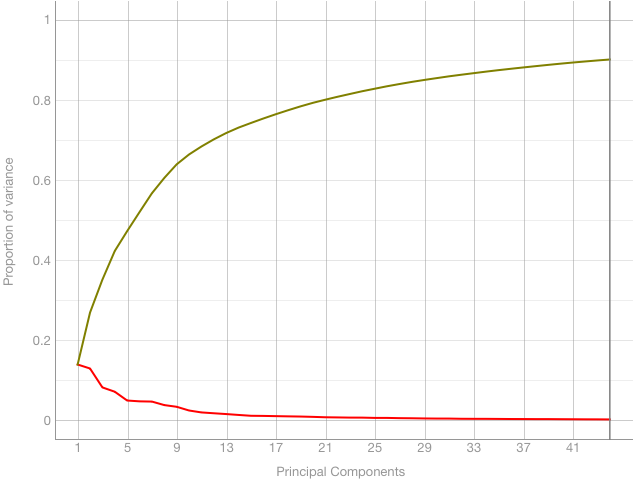
谢谢
Stack Overflow用户
发布于 2016-04-06 09:39:11
可能与Orange的PCA预处理程序或加载数据的方式有关。PCA包含以下两个预处理器:
- 连续化(用于使范畴化,或确定为范畴的值连续化,例如通过一次热转换),以及
- 估算(例如,用平均值替换nans )。
确保在不使用nan值和使用橘子三线标头的情况下加载数据,将所有特性标记为连续的,这样就不会进行转换。
Stack Overflow用户
发布于 2018-05-16 13:36:32
梅比的差异是由于雪橇的normalisation.The之一被皮尔逊std (n-1)除以,而不是std (n).It可以解释小样本情况下的小差异。
检查一下是不是性病
df
df2 = df.mean()
df2 = pd.DataFrame(df2,columns = ['Mean'])
#Calculer l'ecart type de chaque variable
df3 = df.std()
df3 = pd.DataFrame(df3,columns = ['Standard Deviation'])
#Centrer la matrice : faire la difference entre la matrice df et la moyenne de chaque variable
df4 = df.sub(df.mean(axis=0), axis=1)
#Reduire la matrice : diviser la matrice centree par son ecart type
import numpy as np
df5 = df4.divide(df.std(axis=0), axis=1)
df5 = df5.replace(np.nan, 0)雪橇进口预处理中的Pearson std
df=pd.DataFrame(preprocessing.scale(df), index = df.index, columns = df.columns)页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/36401290
复制相关文章
相似问题

