问wav文件整数样本的移位频率(使用FFT)

EN

我想对一个.wav文件进行频移。

所以你有一个音频，这意味着一个真实值的信号。

实值信号的谱与f=0是对称的，即它的傅里叶变换具有hermitian对称性。

如果现在移动输入光谱(蓝色)，结果(红色)就会失去对称性，即产生的信号不再是真实的：

​

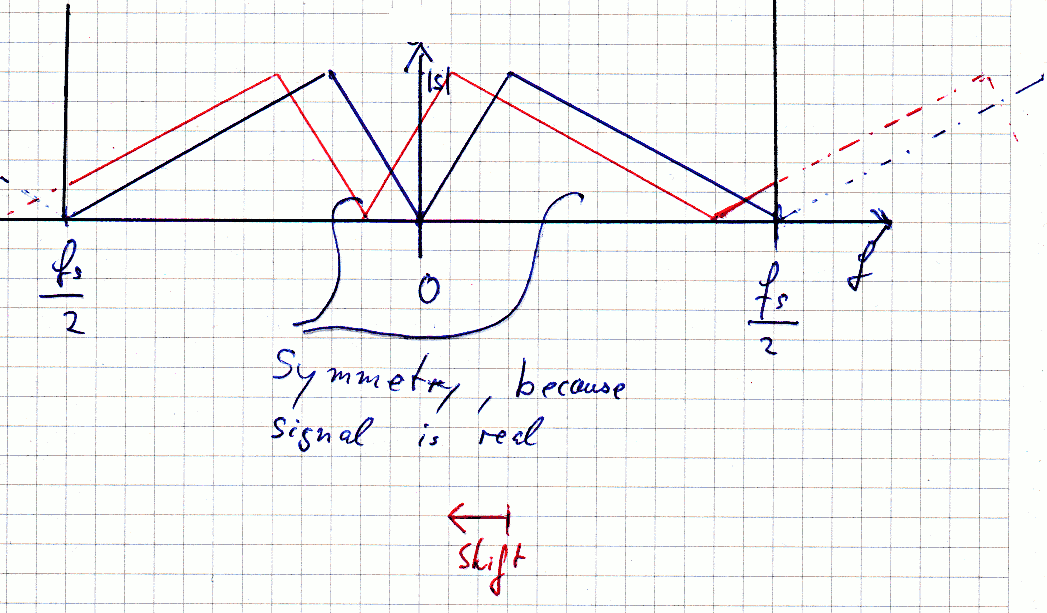
注意事情是如何，通过混叠，循环，所以你“移出”尼奎斯特范围将出现在相反的一端。在我的例子中，这意味着您得到了意想不到的高频组件！

我遇到的问题是FFT使用复数，而.wav文件有整数值。所以我想要做一个频移，这意味着我必须进行一个直接变换和一个逆变换，问题是，逆变换没有给我整数值(它给我复杂的值)，但是我需要.wav文件样本的整数值。

确实是这样！那是因为你换班的结果不再是真正的信号了。

然而，你能做的是：

1. 移位(无论是在时间域还是在频域--老实说，在时间域上这样做会更容易！)只需将n_th样本乘以_exp(2jπf_shift/f_πn)。
2. 应用复杂的带通滤波器，移除频率0；f_sample /2-移位以外的所有内容。这给了你所谓的分析信号(即仅仅是正频率)，它仍然不是实值的，因为它是不对称的。
3. 扔掉想象的部分，现在不会改变你的信号信息-它只是一半的能量，给你一个对称的光谱，和一些东西，你可以写到一个.wav文件。

现在，整个“通过FFT在频域上做这件事”是软件无线电世界中人们非常习惯的一种方法--他们一直在处理复杂的基带信号。

如何解释逆变换的值？

它们是一个复杂的信号。如注释中所建议的，忽略想象的部分会导致负频率中包含的能量被镜像到你的正频率上(以及相反的方向)，而且很可能不是你想要的--除非：

• 你已经确保在这个“对称化”之前，f=0两边的能量是0，所以没有什么不好的事情发生。
• 你确保了你有选择地改变了负的和正的频率，所以，对称性被保留了。注意，这不是整个频域的“简单”移位，而是两个选择性移位；这些移位区域的选择有一个形状，可以归结为使用一个窗口。如果你只是“选择”或“不选择”每个垃圾箱的移动，你有效地应用了一个矩形窗口-与所有吉普的现象，你可能会招致。