NumPy IFFT在OaA卷积算法中引入黑条
NumPy IFFT在OaA卷积算法中引入黑条
提问于 2016-06-12 05:59:05
我很难诊断和修正这个错误。我正在尝试编写OaA算法,描述了在本文中。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
""" Quick implementation of several convolution algorithms to compare times
"""
import numpy as np
import _kernel
from tqdm import trange, tqdm
from PIL import Image
from scipy.misc import imsave
from time import time, sleep
class convolve(object):
""" contains methods to convolve two images """
def __init__(self, image_array, kernel, back_same_size=True):
self.array = image_array
self.kernel = kernel
# Store these values as they will be accessed a _lot_
self.__rangeX_ = self.array.shape[0]
self.__rangeY_ = self.array.shape[1]
self.__rangeKX_ = self.kernel.shape[0]
self.__rangeKY_ = self.kernel.shape[1]
# Ensure the kernel is suitable to convolve the image
if (self.__rangeKX_ >= self.__rangeX_ or \
self.__rangeKY_ >= self.__rangeY_):
raise ValueError('Must submit suitably-sized arrays')
if (back_same_size):
# pad array for convolution
self.__offsetX_ = self.__rangeKX_ // 2
self.__offsetY_ = self.__rangeKY_ // 2
self.array = np.lib.pad(self.array, \
[(self.__offsetY_, self.__offsetY_), \
(self.__offsetX_, self.__offsetX_)],\
mode='constant', constant_values=0)
# Update these
self.__rangeX_ = self.array.shape[0]
self.__rangeY_ = self.array.shape[1]
else:
self.__offsetX_ = 0
self.__offsetY_ = 0
# to be returned instead of the originals
self.__arr_ = np.zeros([self.__rangeX_, self.__rangeY_])\
def spaceConv(self):
""" normal convolution, O(N^2*n^2). This is usually too slow """
# this is the O(N^2) part of this algorithm
for i in trange(self.__rangeX_):
for j in xrange(self.__rangeY_):
# Now the O(n^2) portion
total = 0.0
for k in xrange(self.__rangeKX_):
for t in xrange(self.__rangeKY_):
total += \
self.kernel[k][t] * self.array[i+k][j+t]
# Update entry in self.__arr_, which is to be returned
# http://stackoverflow.com/a/38320467/3928184
self.__arr_[i][j] = total
return self.__arr_[self.__offsetX_\
:self.__rangeX_ - self.__offsetX_,\
self.__offsetY_\
:self.__rangeY_ - self.__offsetY_]
def spaceConvDot(self):
""" Exactly the same as the former method """
def dot(ind, jnd):
""" perform a simple 'dot product' between the 2
dimensional image subsets. """
total = 0.0
# This is the O(n^2) part of the algorithm
for k in xrange(self.__rangeKX_):
for t in xrange(self.__rangeKY_):
total += \
self.kernel[k][t] * self.array[k + ind, t + jnd]
return total
# this is the O(N^2) part of the algorithm
for i in trange(self.__rangeX_):
for j in xrange(self.__rangeY_):
self.__arr_[i][j] = dot(i, j)
return self.__arr_[self.__offsetX_\
:self.__rangeX_ - self.__offsetX_,\
self.__offsetY_\
:self.__rangeY_ - self.__offsetY_]
def OAconv(self):
""" faster convolution algorithm, O(N^2*log(n)). """
from numpy.fft import fft2 as FFT, ifft2 as iFFT
# solve for the total padding along each axis
diffX = (self.__rangeKX_ - self.__rangeX_ + \
self.__rangeKX_ * (self.__rangeX_ //\
self.__rangeKX_)) % self.__rangeKX_
diffY = (self.__rangeKY_ - self.__rangeY_ + \
self.__rangeKY_ * (self.__rangeY_ //\
self.__rangeKY_)) % self.__rangeKY_
# padding on each side, i.e. left, right, top and bottom;
# centered as well as possible
right = diffX // 2
left = diffX - right
bottom = diffY // 2
top = diffY - bottom
# pad the array
self.array = np.lib.pad(self.array, \
((left, right), (top, bottom)), \
mode='constant', constant_values=0)
divX = self.array.shape[0] / float(self.__rangeKX_)
divY = self.array.shape[1] / float(self.__rangeKY_)
# Let's just make sure...
if not (divX % 1.0 == 0.0 or divY % 1.0 == 0.0):
raise ValueError('Image not partitionable (?)')
else:
divX = int(divX)
divY = int(divY)
# a list of tuples to partition the array by
subsets = [(i*self.__rangeKX_, (i + 1)*self.__rangeKX_,\
j*self.__rangeKY_, (j + 1)*self.__rangeKY_)\
for i in xrange(divX) \
for j in xrange(divY)]
# padding for individual blocks in the subsets list
padX = self.__rangeKX_ // 2
padY = self.__rangeKY_ // 2
self.__arr_ = np.lib.pad(self.__arr_, \
((left + padX, right + padX), \
(top + padY, bottom + padY)), \
mode='constant', constant_values=0)
kernel = np.pad(self.kernel, \
[(padY, padY), (padX, padX)], \
mode='constant', constant_values=0)
# We only need to do this once
trans_kernel = FFT(kernel)
# transform each partition and OA on conv_image
for tup in tqdm(subsets):
# slice and pad the array subset
subset = self.array[tup[0]:tup[1], tup[2]:tup[3]]
subset = np.lib.pad(subset, \
[(padY, padY), (padX, padX)],\
mode='constant', constant_values=0)
trans_subset = FFT(subset)
# multiply the two arrays entrywise
subset = trans_kernel * trans_subset
space = iFFT(subset).real
# overlap with indices and add them together
self.__arr_[tup[0]:tup[1] + 2 * padX, \
tup[2]:tup[3] + 2 * padY] += space
# crop image and get it back, convolved
return self.__arr_[self.__offsetX_ + padX + left \
:padX + left + self.__rangeX_ \
- self.__offsetX_, \
self.__offsetY_ + padY + bottom \
:padY + bottom + self.__rangeY_ \
- self.__offsetY_]
def OSconv(self):
""" Convolve an image using OS """
from numpy.fft import fft2 as FFT, ifft2 as iFFT
pass
def builtin(self):
""" Convolves using SciPy's convolution function - extremely
fast """
from scipy.ndimage.filters import convolve
return convolve(self.array, self.kernel)
if __name__ == '__main__':
try:
import pyplot as plt
except ImportError:
import matplotlib.pyplot as plt
image = np.array(Image.open('spider.jpg'))
image = np.rot90(np.rot90(np.rot90(image.T[0])))
times = []
#for i in range(3, 21, 2):
kern = _kernel.Kernel()
kern = kern.Kg2(11, 11, sigma=2.5, muX=0.0, muY=0.0)
kern /= np.sum(kern) # normalize volume
conv = convolve(image, kern)
#
# # Time the result of increasing kernel size
# _start = time()
convolved = conv.OAconv()
#convolved = conv.builtin()
# _end = time()
# times.append(_end - _start)
#x = np.array(range(3, 21, 2))
#plt.plot(range(3, 21, 2), times)
#plt.title('Kernel Size vs. spaceConv time', fontsize=12)
#plt.xlabel('Kernel Size (px)', fontsize=12)
#plt.ylabel('Time (s)', fontsize=12)
#plt.xticks(x, x)
#plt.show()
#conv = convolve(image[:2*kern.shape[0],:5*kern.shape[1]], kern)
plt.imshow(convolved, interpolation='none', cmap='gray')
plt.show()
#imsave('spider2', convolved, format='png')但是现在,当我调用它时,我得到了一个测试图像中的黑条,如下所示:
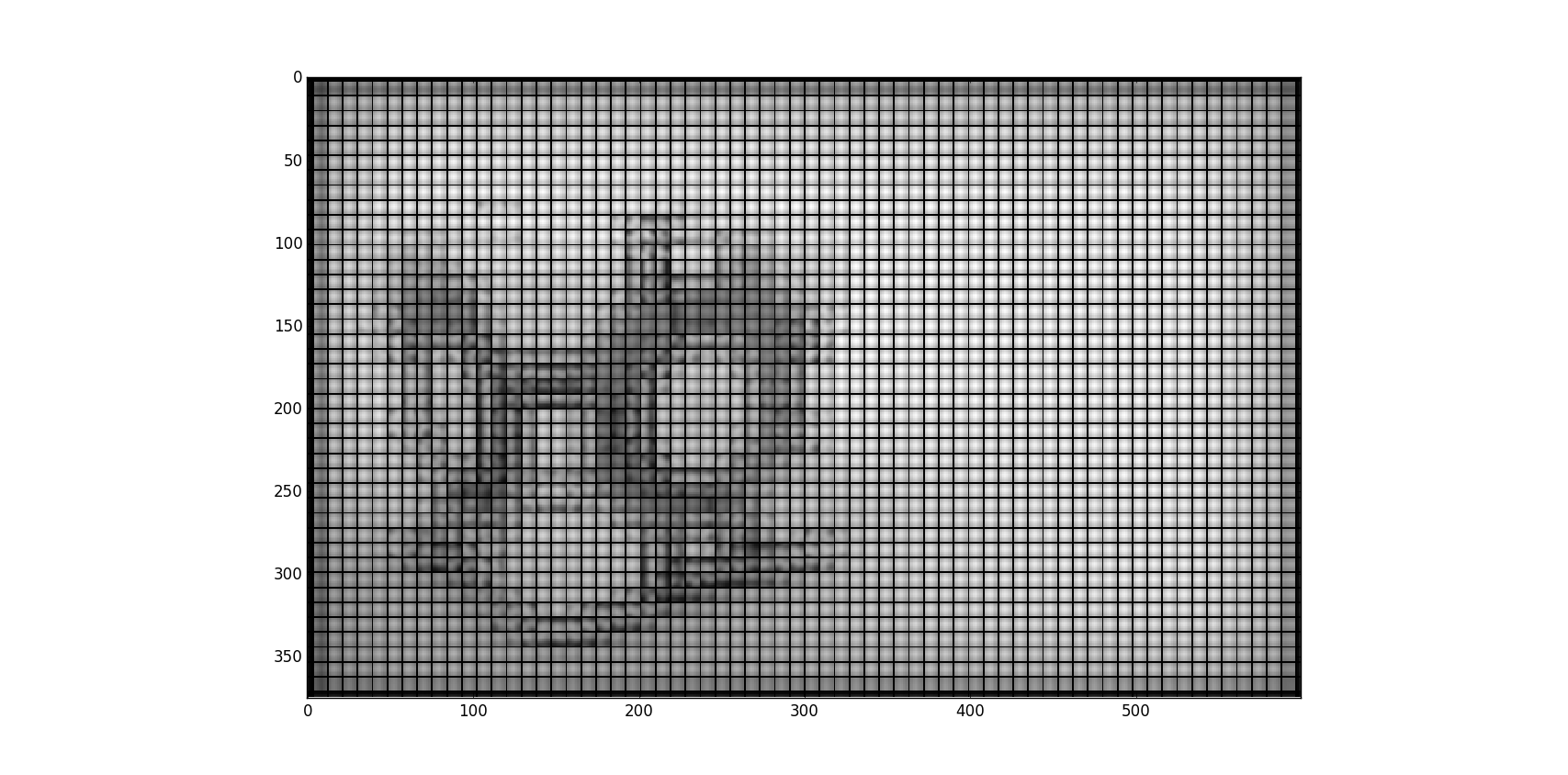
下面是我使用的高斯核的一个例子。
[[ 0. 0.02390753 0.03476507 0.02390753 0. ]
[ 0.02390753 0.06241541 0.07990366 0.06241541 0.02390753]
[ 0.03476507 0.07990366 0.10040324 0.07990366 0.03476507]
[ 0.02390753 0.06241541 0.07990366 0.06241541 0.02390753]
[ 0. 0.02390753 0.03476507 0.02390753 0. ]]我想我已经把问题缩小到乘法和IFFT了
space = np.real(IFFT(transformed_kernel*transformed_subset))我认为这与离散高斯核的IFFT有关(出于某种原因)。这很奇怪因为如果我只是在策划
space = np.real(IFFT(transformed_subset))我得到了以下内容(没有黑条,它将其分解回精细的):

如果我画的是相反的,
space = np.real(IFFT(transformed_kernel))我再次得到没有黑条,它似乎把他们放在正确的地方。
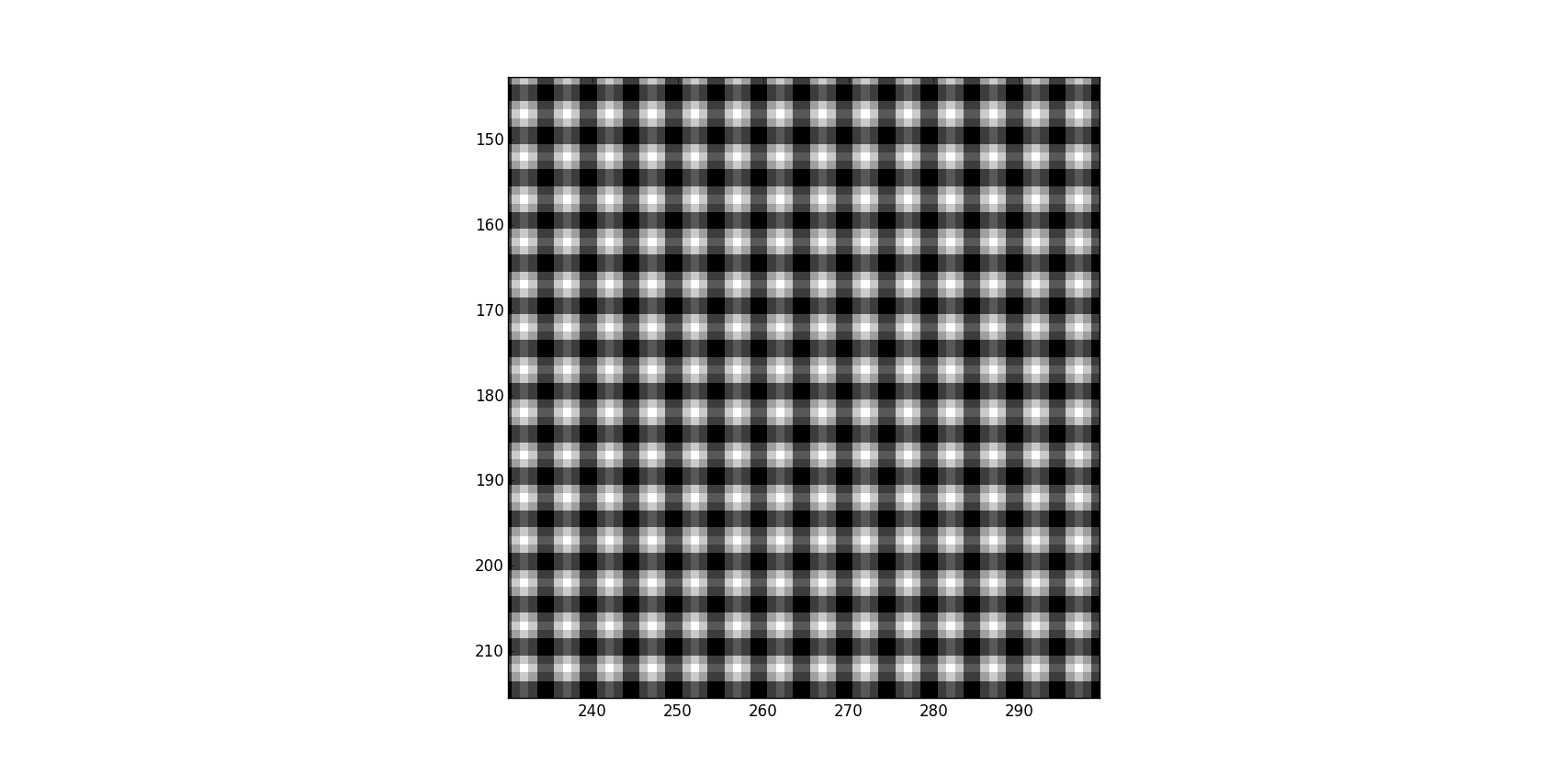
我遗漏了什么?我已经盯着这个看了好几天了,编辑索引什么的,但是我无法摆脱这个标签:
回答 1
Stack Overflow用户
回答已采纳
发布于 2016-07-14 21:28:01
您的问题是,内核似乎处于中间:
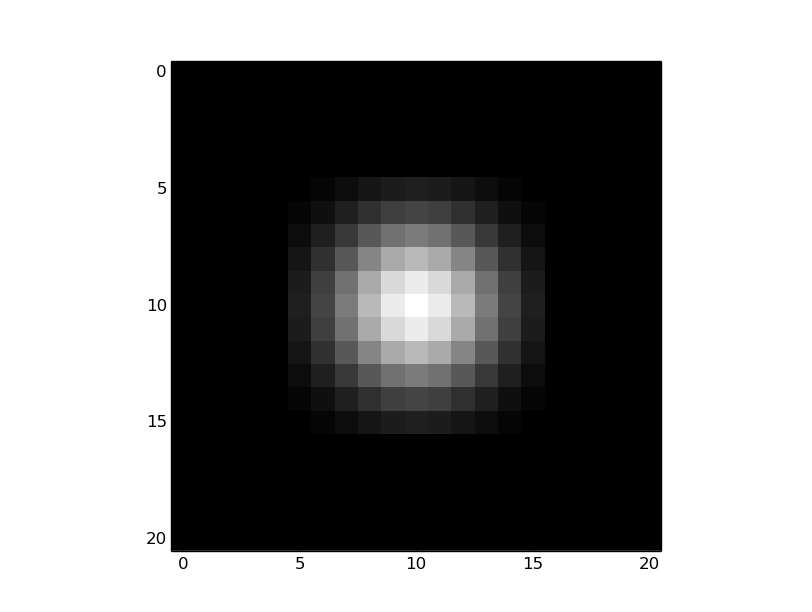
但事实并非如此--还有一个变化(11,11),当你看卷积的结果时,这一点就变得很明显了。内核的中心应该在(0,0)中,并且(由于模块化)内核应该如下所示:
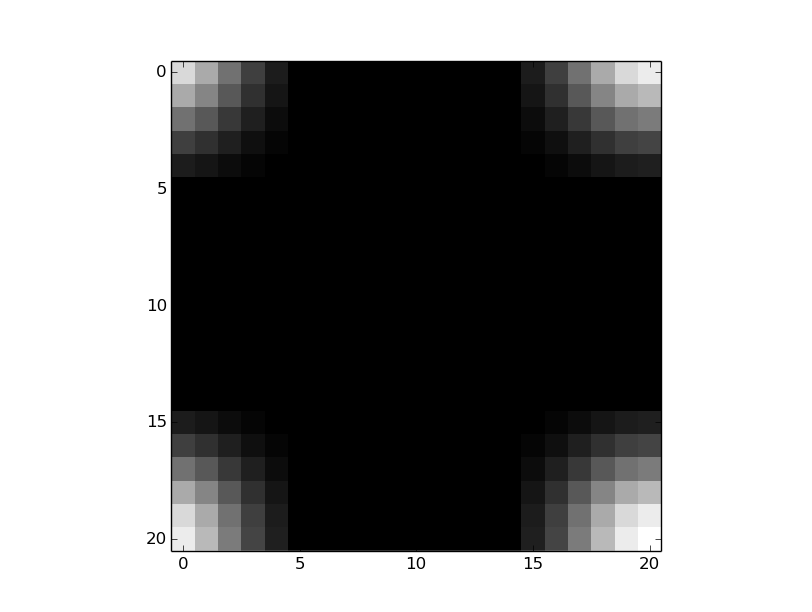
因此,我稍微修改了您的代码(对不起,我从来没有这么多地使用过np,但我希望您能得到要点):
... your code ...
kernel = np.pad(self.kernel, \
[(padY, padY), (padX, padX)], \
mode='constant', constant_values=0)
#Move the kernel center to the origin:
new_kernel=np.full_like(kernel, 0)
X,Y=kernel.shape
X_2=X//2
Y_2=Y//2
for x in xrange(X):
for y in xrange(Y):
n_x=(x+X_2)%X
n_y=(y+Y_2)%Y
new_kernel[n_x,n_y]=kernel[x,y]
# We only need to do this once
trans_kernel = FFT(new_kernel)# take the transform of the shifted kernel
.... your code ......以及:

没有黑色网格!
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/37771182
复制相关文章
相似问题

