寻找两点之间的最大路径
给定一个无向连通图,旅行者必须从node A多次旅行到node B。每个边都有一个正值,从node A到node B有多条路径。路径的值被定义为该路径中所有边的最小值。如果旅行者通过一条特定的路径从node A到node B,则路径中所有边缘的值都会根据路径的值(即该路径中所有边缘的最小值)而减小。The goal is to find the set of paths that give the maximum sum of values of all paths traveled.
注该图可能包含周期,但路径只能访问节点
once。
举个例子,假设有4个节点( A、B、C、D ),旅行者必须从A到D。假设所走过的路径是A->B->D,和
edge_A_B =5 edge_B_D =3
则路径的值为
最小(edge_A_B,edge_B_D) =3
走完这条路之后
edge_A_B =5-3=2 edge_B_D =3-3=0
旅行者必须再次使用更新的边缘值从A到D旅行,直到从A到D的所有路径都有0的值。
回答 1
Stack Overflow用户
发布于 2016-07-05 23:43:03
您的问题非常类似于Max-Flow/Min-Cut-Problem.
因为你可以走每条路的次数是由最小值的边决定的,所以最大值是由图的两个较小的顶点集V和W中的划分(“割集”)所限制的,而起始节点在V中,末端节点在W中,所有边的值都是从V到W的,这是因为为了从开始到结束,旅行者必须遍历连接V和W的边缘,这意味着如果这些边有值0,那么旅行者就没有更多的路径可供旅行者选择。
检查由格言制作的图像
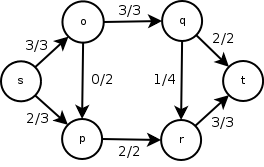
右数字表示边的值,左数表示流(或在您的情况下所走的路径)。这里,切割的最小值是5,这是o与q或q和t之间的垂直切割。因此,最大流(或在您的情况下,所有路径的最大值)也是5。由于传入流的值等于传出流的值(除了开始和结束节点外),所以很容易找到他后来走过的路径。在这种情况下,它是{{s, o, q, t}, {s, o, q, r, t}, {s, p, r, t}}。
https://stackoverflow.com/questions/38214146
复制相似问题

