哈希函数在密码学与特征中的应用
我只是开始学习特性散列,所以我需要帮助来理解是否可以应用以地图表示的散列函数。
而Tent映射的一个应用是在密码学中--论文1:基于神经密码下载链接的哈希函数的实现。
在特征哈希中,设x是D维的一个数据点,即它有D个元素数。在特征哈希中,使用线性散列函数将D维数据点转换为较低k维数据点,从而保持降维特征空间中的距离。哈希位k是通过操作h_k(x) = sign(y(x)) = sign(f(w_k^Tx +b))获得的。输出h(x)为0或1位。
本质上,我们是通过创建随机超平面来对数据点x属于0或1类进行分类。
特征哈希函数在降维方面有多种选择:f = tanh()或简单随机抽样,以获得超平面。另一种选择是在数据不是线性可分的情况下使用内核函数。这种哈希函数/technique是利用核函数来实现的,采用高斯径向基函数作为核函数是一种普遍的选择。
- 问:在第1篇中,作者使用单位区间上分段线性的非对称帐篷映射地图作为传递函数。在我看来,本文中使用Tent Map的哈希公式类似于散列方程(1)。如何应用分段线性函数,即应用此映射创建超平面以进行特征哈希? 还是我混淆了这两个概念?
回答 1
Stack Overflow用户
发布于 2016-09-27 11:39:36
特征散列需要一个散列函数,这样它就能够.它的哈希技巧!
它将对每个图像进行散列,因此您需要一个哈希函数,它将接受图像(即D维的特征/向量)并生成一个整数值。
注意:我认为您混淆了第二个单位输出哈希函数ξ,w.r.t。结果将是二进制的。一旦获得初始方法的流程,ξ()就很容易掌握,因为这只是一个减少哈希冲突的优化。
现在,让我们看一看Tent_map_2的行为:
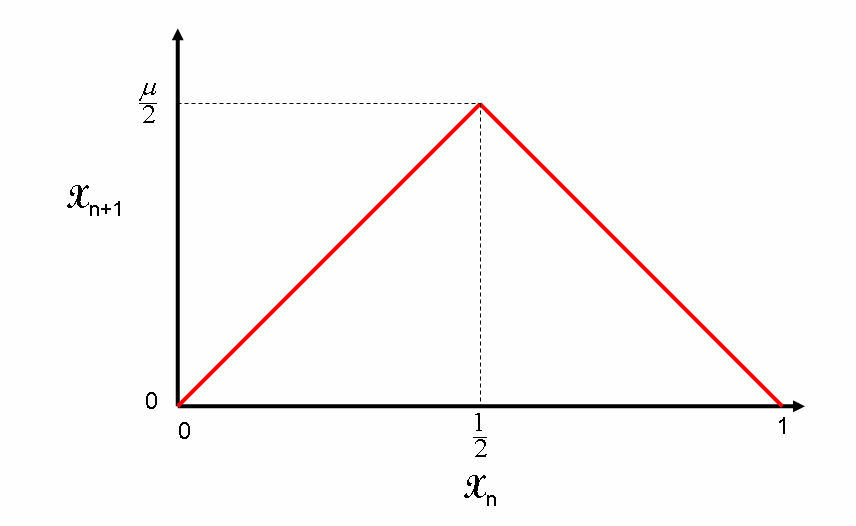
正如你所看到的,它是一个实值函数。
它以一个数字作为输入,给出一个数字作为输出。因此,一个朴素的帐篷地图不能散列一个向量(在我们的例子中是一个图像)。有许多方法可以增强Tent Map以处理向量,最简单的方法是:
实现一个tentMap函数,例如tentMap(),它将实现tentMap的逻辑。您可以将Tent的返回值处理为0,其余值(即>= 0.5)为1,但如果您愿意,您可以做更复杂的事情。
现在,对于图像,您可以这样做:
def tentMapVector(image):
results = []
for i in image:
results.append(tentMap(i))
# now 'results' contains D integers
# it needs to be hashed to a single integer
# you could treat 'results' as a string and
# use one of the numerous hash function to hash that string
return hashString(results)tentMapVector()应该在维基百科的实现中取代hash()。您可能想阅读它的示例,非常有用。
特性似乎不需要维数约简,它应该不需要降维,但当数据留在高维空间(通常是图像)时,您应该尝试将维数从256降到128。
例如,您可以使用来自科学知识-学习的PCA()或任何其他库。
https://stackoverflow.com/questions/39629006
复制相似问题

