问凸多面体(方金字塔)内三维点的检测算法

EN

我正在寻找健壮的碰撞检测算法，并发现了一本很棒的书，名为“实时碰撞检测”，作者是克里斯特·埃里克森。我试图使用一种特定的算法来检查给定的点是否在凸多面体内(在三维空间中，这些是方形的金字塔、立方体和四面体(也就是所有边都是三角形的金字塔)。在我的例子中，我有一个方形金字塔。该点的验证是通过使用给定数量的半空间的交点体积，并确定该点是在前面还是后面的所有平面是跨越多面体的边。我很难理解参数n (见下文)的用法，它表示给定多面体的半空间数：

// Test if point p inside polyhedron given as the intersection volume of n halfspaces
int TestPointPolyhedron(Point p, Plane *h, int n) {
    for (int i = 0; i < n; i++) {
        if(DistPointPlane(p, h[i]) > 0.0f) return 0;
    }
    return 1;
}

用DistPointPlane(...)计算给定点与平面之间的距离

float DistPointPlane(Point q, Plane p) {
    return Dot(q, p.n) - p.d;
}

Plane是一种在三维空间中表示平面的结构

struct Plane {
    Vector n; // Plane normal. Point X on the plane satisfies Dot(n, X) = d
    float d;  // d = dot(n, p) for a given point on the plane
}

Plane ComputePlane(Point a, Point b, Point c) {
    Plane p;
    p.n = Normalize(Cross(b - a, c - a));
    p.d = Dot(p.n, a);
    return p;
}

该算法所做的基本工作如下：

1. 对于给定的点，计算它与凸多面体的每个平面的距离。
2. 检查距离是负的还是正的
   1. 如果距离是负的，那么点就在飞机正常的另一边，所以它就在后面。
   2. 否则点在飞机的同侧，所以它就在飞机的前面

​

1. 如果点在给定多面体的所有平面后面，则它位于在内，否则它位于之外的。

就我所知的一个方形金字塔来说，有10个半空间，因为我们有4个边和一个基，每个代表一个独立的平面(总共有5个平面)，它把三维空间分成两个半空间(5 planes * 2 = 10 halfspaces)。我不明白的是，在上面算法的代码中使用了n。它用作循环的终止条件，循环遍历Plane实例数组。然而，如前所述，有10个半空间。

经过一番挖掘，我想到的一件事是，两个平面之间的交点是一条线(金字塔的边缘)。进一步引用沃尔夫拉姆·马西尔

要唯一地指定行，还需要在行上找到一个特定的点。这可以通过在两个平面上同时找到一个点来确定。

每个金字塔的顶点都满足这一要求，因为对于任何给定的两边(包括底部)，我们都得到了一条位于金字塔的两个顶点之间的直线。因此，在交集方面，我们确实有5 (4表示底部，1表示顶点)，但是书中的文本(包括函数实现上面的注释)含糊不清，阅读它可能会产生错误的想法(至少这是我的情况)。

我的思路是否接近真理，还是我在数学知识方面遗漏了很大一部分？

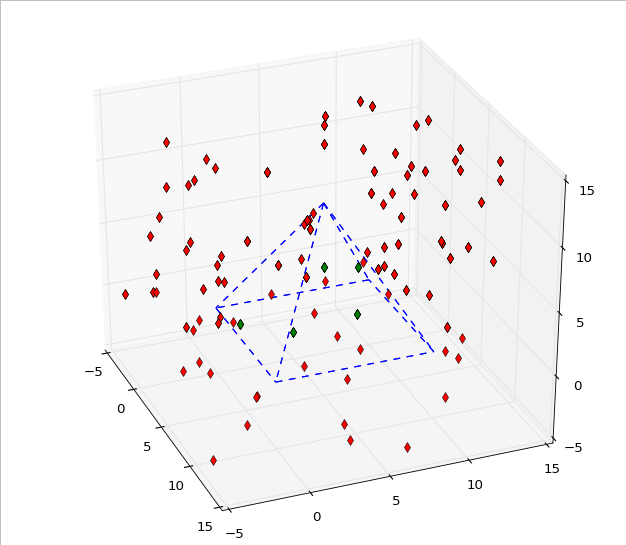
我已经将代码移植到Python3中，并修改了算法，使其只遍历我的平面列表，而不带额外的参数(如果我的想法是正确的，它基本上与最初的参数相同)，并用matplotlib绘制了它。它非常好，但我仍然想知道我是否正确地理解了它：

​

​