用遗传算法收敛到2变量函数的全局极小值
用遗传算法收敛到2变量函数的全局极小值
提问于 2016-09-30 11:44:23
我使用Visual C++作为平台,试图收敛到全局最小值。
假设这个函数是一个黑盒函数,如果我输入(x,y),得到z。
而且,所使用的算法是一个实值遗传算法,我不是将样本转换为二进制代码,而是将其转换为浮点数。
https://karczmarczuk.users.greyc.fr/TEACH/IAD/GenDoc/carrGenet.pdf
我使用了附录B中提到的算法来求2-变量函数的最小值。
f(x,y) =z
我做了一个网格值搜索,以得到问题的图表。我把图表附上去了。
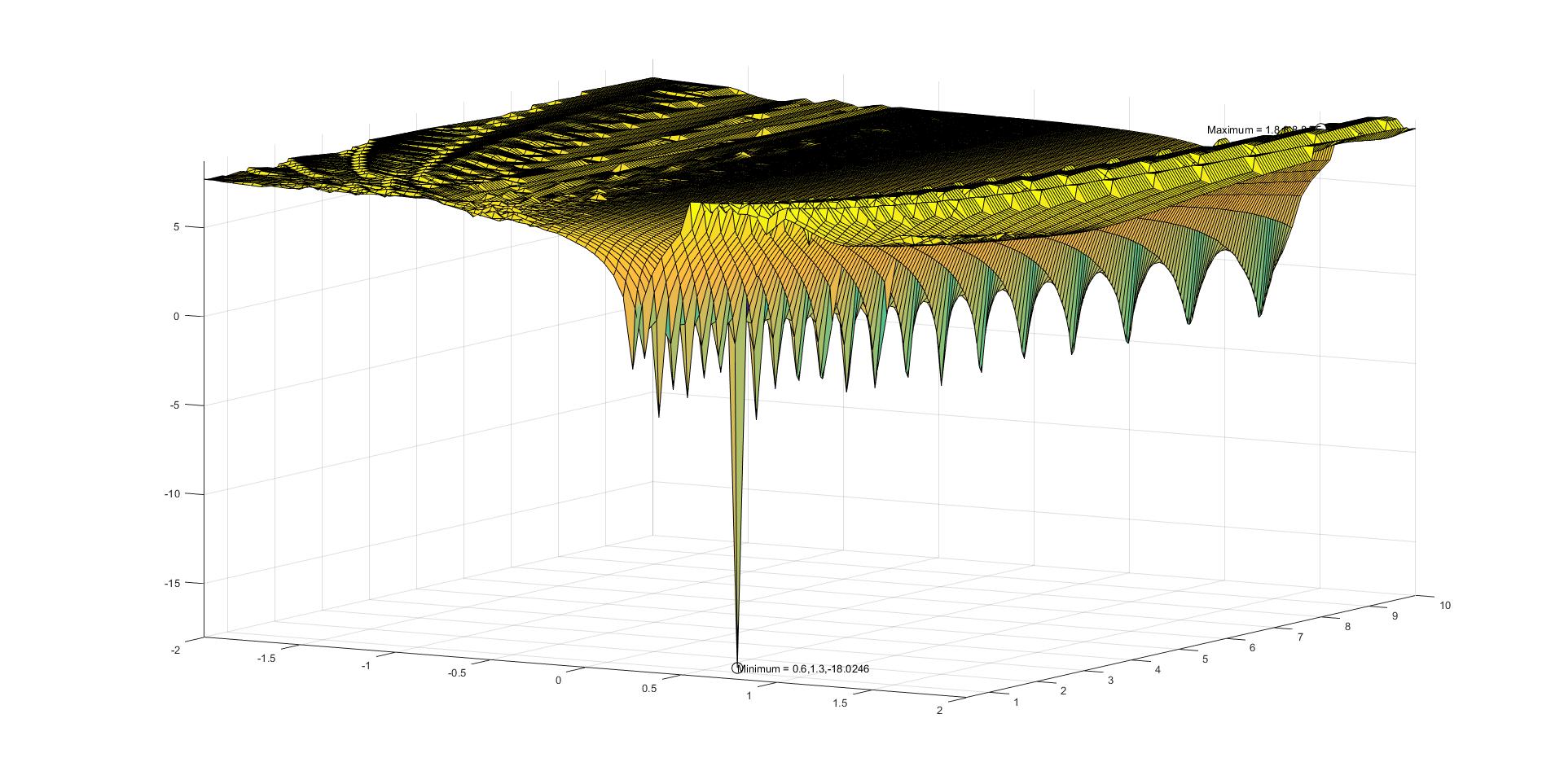
在这里,图的最小值(从图中可以看到)仅位于的一个点 (0.6,1.3)。
如果使用离散值(x,y)的倍数为0.1,则该算法收敛。就像。0.8,0.9,2.2,5.6等,但否则它不收敛。
我是否可以修改图形以适应算法,或者如果我可以修改算法来最小化函数呢?
回答 2
Stack Overflow用户
发布于 2016-09-30 12:36:11
你的全局最优在这里是非常尖锐的。你需要很大的运气才能陷进去。很多随机个体几乎没有找到它的机会)。
如果你设法得到一个人在斜坡上,遗传算法将收敛到最优。因此,我建议获得一个更平滑的最优值,或者尝试更多的随机值。
Stack Overflow用户
发布于 2016-10-03 20:03:23
我不确定你是否考虑了黑匣子中的随机数生成器,那么你的输入函数是否有结构,你可以用随机初始化或者随机突变的方式来表示?
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/39790777
复制相关文章
相似问题

