Python谱分析
我试图估计一个心电信号的心率变异性的PSD。为了测试我的代码,我从幻想曲心电数据库中提取了R间隔。我提取的信号可以接入这里。为了计算PSD,我使用welch方法,如下所示:
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import welch
ibi_signal = np.loadtxt('fantasia-f1y01-RR.txt')
t = np.array(ibi_signal[:, 0]) # time index in seconds
ibi = np.array(ibi_signal[:, 1]) # the IBI in seconds
# Convert the IBI in milliseconds
ibi = ibi * 1000
# Calculate the welch estimate
Fxx, Pxx = welch(ibi, fs=4.0, window='hanning', nperseg=256, noverlap=128)接下来,计算曲线下的面积,以估计不同HRV波段的功率谱,如下所示
ulf = 0.003
vlf = 0.04
lf = 0.15
hf = 0.4
Fs = 250
# find the indexes corresponding to the VLF, LF, and HF bands
ulf_freq_band = (Fxx <= ulf)
vlf_freq_band = (Fxx >= ulf) & (Fxx <= vlf)
lf_freq_band = (Fxx >= vlf) & (Fxx <= lf)
hf_freq_band = (Fxx >= lf) & (Fxx <= hf)
tp_freq_band = (Fxx >= 0) & (Fxx <= hf)
# Calculate the area under the given frequency band
dy = 1.0 / Fs
ULF = np.trapz(y=abs(Pxx[ulf_freq_band]), x=None, dx=dy)
VLF = np.trapz(y=abs(Pxx[vlf_freq_band]), x=None, dx=dy)
LF = np.trapz(y=abs(Pxx[lf_freq_band]), x=None, dx=dy)
HF = np.trapz(y=abs(Pxx[hf_freq_band]), x=None, dx=dy)
TP = np.trapz(y=abs(Pxx[tp_freq_band]), x=None, dx=dy)
LF_HF = float(LF) / HF
HF_LF = float(HF) / LF
HF_NU = float(HF) / (TP - VLF)
LF_NU = float(LF) / (TP - VLF)然后我绘制PSD并得到下面的图
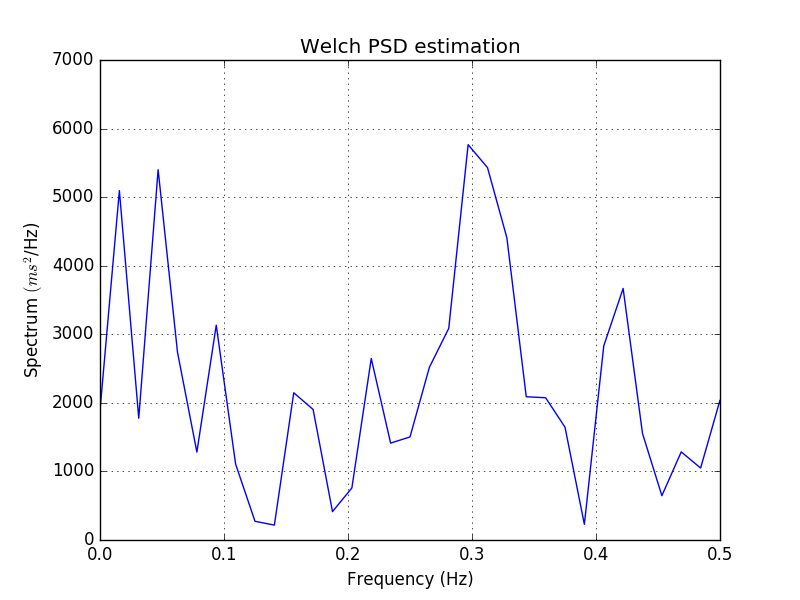
一开始我很强硬,结果看上去没问题。然而,当我把我的输出和Kubios的输出进行比较时,我注意到了它们之间的差异。下图显示了Kubios计算的PSD的期望值
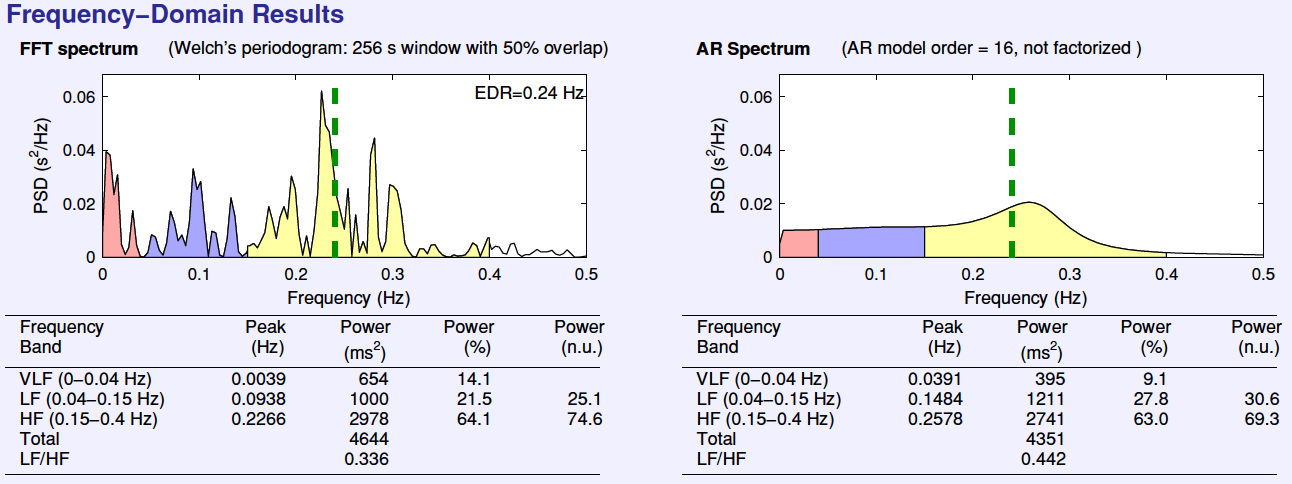
也就是说,这两个情节在视觉上是不同的,它们的价值也有很大的不同。为了证实这一点,我的数据的打印清楚地表明我的计算是错误的。
ULF 0.0
VLF 13.7412277853
LF 45.3602063444
HF 147.371442221
TP 239.521363002
LF_HF 0.307795090152
HF_LF 3.2489147228
HF_NU 0.652721029154
LF_NU 0.200904328012因此,我想知道:
- 有人能建议我读一份文件来提高我对光谱分析的理解吗?
- 我的方法怎么了?
- 如何为welch函数选择最合适的参数?
- 虽然这两幅图的形状是相同的,但数据却完全不同。我怎样才能改善这一点?
- 有没有更好的方法来解决这个问题?我正在考虑使用估计,但我正在等待至少得到韦尔奇方法的工作。
回答 1
Stack Overflow用户
发布于 2016-10-27 10:53:03
这里的问题是,您没有正确处理您的信号的采样。在welsch调用中,您考虑采样频率为4Hz的定期采样信号。如果你看一下时间向量t
In [1]: dt = t[1:]-t[:-1]
In [2]: dt.mean(), np.median(dt)
Out[2]: 0.76693059125964014, 0.75600000000000023
In [3]: dt.min(), dt.max()
Out[3]: (0.61599999999998545, 1.0880000000000081)因此,您的信号不定期取样。因此,您需要把它放入acount,否则您不能正确地估计PSD,这会给您糟糕的估计。
第一个修正应该是正确使用welsch中的参数fs。此参数指示给定信号的采样频率。将其放在4中意味着您的时间向量应该是一个常规的[0, .25, .5, .75, .1, ....]。一个更好的估计将是dt或len(t)/(t.max()-t.min())的中位数,也就是4/3的中间值。这给出了更好的PSD估计和对某些常数的正确排序,但与Kubios值相比仍然是不同的。
为了得到正确的估计,你应该使用一个非均匀DFT。实现这种转换的包可以找到这里。对于这个包,文档非常神秘,但是您需要使用伴随方法来获得傅里叶变换,而不需要缩放问题:
N = 128 # Number of frequency you will get
M = len(t) # Number of irregular samples you have
plan = NFFT(N, M)
# Give the sample times and precompute variable for
# the NFFT algorithm.
plan.x = t
plan.precompute()
# put your signal in `plan.f` and use the `plan.adjoint`
# to compute the Fourier transform of your signal
plan.f = ibi
Fxx = plan.adjoint()
plt.plot(abs(Fxx))在这里,估计数似乎与Kubios的估计数不一致。估计可能是因为你对整个信号做了psd估计。您可以尝试使用韦尔奇技术结合这个nfft,平均估计加窗信号,因为它不依赖于快速傅立叶变换,但任何估计的私营部门司。
https://stackoverflow.com/questions/40086784
复制相似问题

