在指定的x值范围内,如何将线性斜率与图相匹配?
在指定的x值范围内,如何将线性斜率与图相匹配?
提问于 2016-11-10 13:39:01
例如,这里有一个数据集:
X: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Y: 20, 21, 22, 26, 32, 41, 39, 36, 29, 23我想我应该使用NumPy polyfit函数,但不确定。例如,我如何才能得到x(3)和x(6)之间的线性拟合?
在我脑子里想的应该是:rise/run = (41-22)/(6-3) = 6.3333333...
每次我以.txt文件的形式读取数据集时,我都会处理不同的数据集,所以如果有人向我展示这样做的一般方法,我会非常感激,然后我可以将它应用到所有未来的数据集中。
回答 1
Stack Overflow用户
发布于 2016-11-10 14:12:23
我想你想要一个最小二乘的拟合,这就是多重拟合给你的。
要做到这一点,您只需将两个列表传递给polyfit,即x值、y值,并且必须设置所需多项式的顺序。所以对于你的例子来说,这将会是
import numpy as np
x = [3, 6]
y = [22, 41]
coeffs = np.polyfit(x, y, 1)
# get the y values of the resulting line
x = np.arange(1,11)
y_line = x * coeffs[0] + coeffs[1]关于您的进一步问题,您需要考虑的输出多适合。
numpy.polyfit的文档显示
该解决方案最小化了平方误差。 E= \sum_{j=0}^k =p(X_j)- y_j|^2 在方程式中: x**n *p+.+x* pn-1 + pn =y x1**n *p+.+ x1 * pn-1 + pn = y1 ..。 xk**n *p+.+ xk * pn-1 + pn = yk
我们使用了一个非常简单的例子,因为为了得到一条直线,我们有一个一阶多项式,即n=1。
这意味着在我们的例子中,y的方程是简单的y[k] = x[k]*p[0]+p[1]。将其与线方程y = k*x+d的一般形式进行比较。您将看到您的行的斜率仅为coeffs[0]。
至于绘图,请参见下面的示例
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1, 11)
y = [20, 21, 22, 26, 32, 41, 39, 36, 29, 23]
poly = np.polyfit(x, y, 1)
y_line = x * poly[0] + poly[1]
print poly[0]
plt.scatter(x, y)
plt.plot(x, y_line)
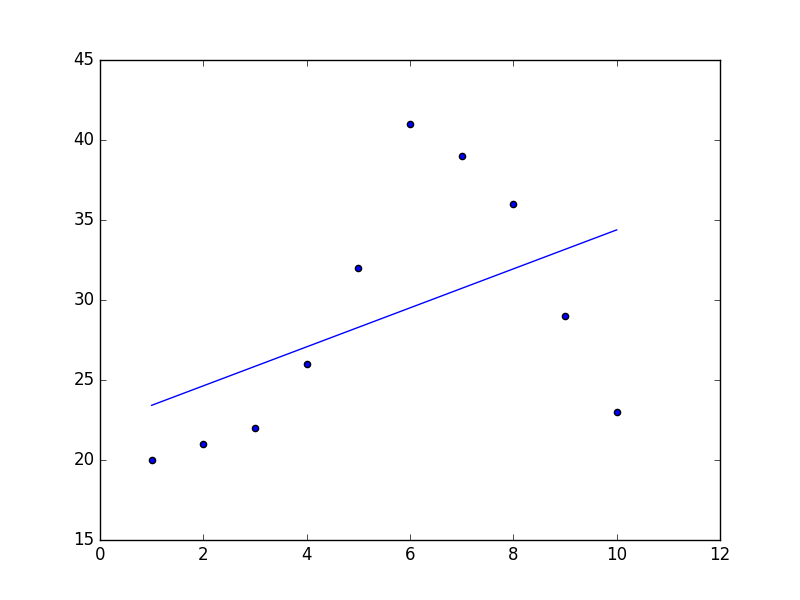
plt.show()从而导致输出
$ python test.py
1.21818181818
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/40529039
复制相关文章
相似问题

