10^-6精度确定嵌套根常数值的Java程序
10^-6精度确定嵌套根常数值的Java程序
提问于 2016-11-23 17:38:45
嵌套根常数定义为:
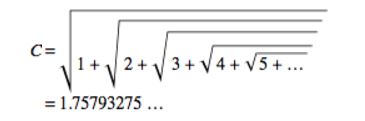
我正在编写一个Java程序来计算10^-6精度的嵌套基常数的值,并打印达到该精度所需的迭代次数。这是我的代码:
public class nested_radical {
public nested_radical() {
int n = 1;
while ((loop(n) - loop(n - 1)) > 10e-6) {
n++;
}
System.out.println("value of given expression = " + loop(n));
System.out.println("Iterations required = " + n);
}
public double loop(int n) {
double sum = 0;
while (n > 0) {
sum = Math.sqrt(sum + n--);
}
return (sum);
}
public static void main(String[] args) {
new nested_radical();
}
}这段代码完成了它应该做的事情,但速度很慢。我应该做些什么来优化这个程序?有人能提出另一种可能的方法来实施这个计划吗?
我还想用MATLAB编写一个类似的程序。如果有人能把这个程序翻译成MATLAB,那就太好了。
回答 1
Stack Overflow用户
回答已采纳
发布于 2016-11-23 21:41:07
我在这段代码中做了一些修改,现在它存储loop(n - 1)的值,而不是每次计算它。现在这个程序看起来比以前优化得多了。
public class nested_radical {
public nested_radical() {
int n = 1;
double x = 0, y = 0, p = 1;
while ( p > 10e-6) {
y=x; /*stored the value of loop(n - 1) instead of recomputing*/
x = loop(n);
p = x - y;
n++;
}
System.out.println("value of given expression = " + x);
System.out.println("Iterations required = " + n);
}
public double loop(int n) {
double sum = 0;
while (n > 0) {
sum = Math.sqrt(sum + n--);
}
return (sum);
}
public static void main(String[] args) {
new nested_radical();
}
}我还成功地在MATLAB中翻译了这段代码。下面是MATLAB的代码:
n = 1;
x = 0;
p = 1;
while(p > 10e-6)
y = x;
sum = 0;
m=n;
while (m > 0)
sum = sqrt(sum + m);
m = m - 1;
end
x = sum;
p = (x-y);
n = n + 1;
end
fprintf('Value of given expression: %.16f\n', x);
fprintf('Iterations required: %d\n', n);页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/40770987
复制相关文章
相似问题

